Cho góc XOY điểm M thuộc tia phân giác của góc qua M kẻ đuoengf thẳng vuông góc OX tại A cắt OX tại C. Qua M kẻ đường thẳng vuông góc B cắt OX tại điểm D A. Cm OA bằng OB B. CM OM là đường trung trực AB C. Tìm tập hợp các điểm đều D và C D. Cm AB song song vs CD E. qua D kẻ đường thẳng A vuông góc vs OX đường thẳng B vuông góc vs OY. N là giao điểm của A và B Cm Q, M, N thẳng hàng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 2 2017
XÉT TAM GIÁC OAM VÀ TAM GIÁC OMB CÓ
GÓC OAM = GÓC OBM=90*
OM CHUNG LÀ CẠNH HUYỀN CHUNG
MA=MB
=>TAM GIÂC OAM = TA GIÁC OBM (CH GN)
=>OA=OB
=>TAM GIÁC OAB CÂN TẠI A
B, XÉT TAM GIÁC MAD VÀ TAM GIÁC MBE CÓ
GÓC A=GÓC B =90*
GÓC M CHUNG
AD=BE
=>TAM GIÁC MAD=MBE
=>MD=ME
15 tháng 2 2017
XÉT TAM GIÁC OAM VÀ TAM GIÁC OMB CÓ
GÓC A=GÓC B=90*
OM LÀ CẠNH HUYỀN CHUNG
GÓC O CHUNG]
=>TAM GIÁC OAM = TAM GIÁC OMB(CH-GN)
=>OA=OM(CẠNH TƯƠNG ỨNG)
=> TAM GIÁC OAB CÂN TẠI O
B,XÉT TAM GIÁC ADM VÀ TAM GIÁC MBE CÓ
GÓC A = GÓC B=90*
GÓC AMD= GÓC EMB
GÓC M CHUNG
=>TAM GIÁC ADM = TA GIÁC MEB(GCG)
=>MD=ME(đpcm)
28 tháng 12 2017
+) Xét tg ONB và OMA có
OB= OA (gt)
Góc O chung
Góc B = góc A(=90)
=> ∆ OMA (ch - gn)
=> />+) Ta có OA + AN = ON
OB+ BM= OM
Mà OA= OB
/>=> AN = BM
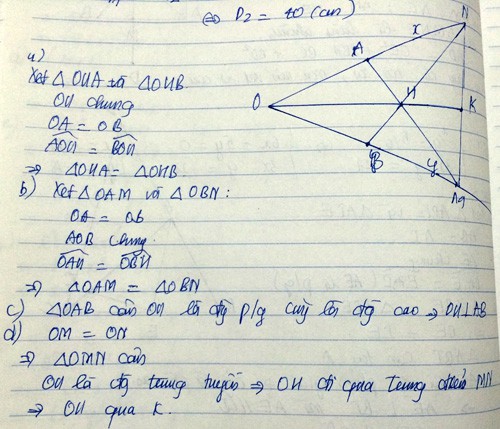
+) XÉT ∆OAH và ∆ OBH
OH cạnh cchung
OA= OB
góc A = góc B
=>∆ OAH= ∆ OBH( cho CGV)
=> AOH= BOH
=> OH là phân giác xOy
ta có (cmt)
=> ∆ ONM cân tại O
OI là trung tuyến => OI là đường cao
OI vuông góc NM(1)
Ta có MA, NB lần lượt vuông góc với Ox, Oy
MA cắt NB tại H
=> H là trực tâm của ∆OMN
=> OH vuông góc NM(2)
từ (1)(2)=> O , H , I thẳng hàng ( qua O chỉ kẻ đc duy nhất 1 đường thẳng vuông góc NM)