cho tứ giác ABCD có MNPQ lần lượt là tring điểm của AB, AC, CD, BD.CM:a)MN//BC và MN=BC/2 b) MN// PQ và MN= PQ .c) tứ giác MNPQ là hinh binh hành
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Nối A với C
Xét tam giác ABC có: M là trung điểm của AB
N là trung điểm của BC
=> MN là đường trung bình của tam giác ABC
=> MN = 1/2 AC (1)
Chứng minh tương tự, ta được: PQ là đường trung bình của tam giác ADC
=> PQ = 1/2 AC (2)
Từ (1)(2) => MN = PQ ( cùng bằng 1/2 AC)
b) Ta có: MN = PQ = MQ = PN (cùng = 1/2 AC = 1/2 BD)
=> MNPQ là hình thoi ( 3)
Mặt khác: AC vuông góc với BD (ABCD là hình thoi)
MN song song với AC
=> Mn vuông góc với BD
Và BD song song với NP
=> MN vuông góc với NP
=> góc MNP = 90 độ (4)
Từ (3) và (4) => MNPQ là hình vuông
Nối AC,BD
a) Ta có:
M là TĐ của AB (gt) ; N là TĐ của BC (gt) \(\Rightarrow\)MN là đường trung bình của tam giác ABC \(\Rightarrow\)MN =\(\frac{1}{2}AC\), MN song song với AC
Tương tự: \(PQ=\frac{1}{2}AC\); PQ song song với AC ; MQ song song với BD, NP song song với BD
nên MN=PQ (đpcm)
b) Theo câu a) ta có :
MN song song với PQ ,MQ song song với NP nên tứ giác MNPQ là hình bình hành (1)
Lại có :AC vuông góc với BD nên MN vuông góc với MQ hay góc M = 90 độ (2)
Từ (1) và (2) tứ giác MNPQ là hình chữ nhật

Đáp án B
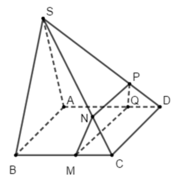
Ta có: MN // BS ⇒ C M C B = C N C S
MQ // CD // AB (do ABCD là hình bình hành nên AB //CD) ⇒ C M C B = D Q D A
NP // CD ⇒ C N C S = D P D S
Do đó: D P D S = D Q D A PQ // SA (Định lý Ta - lét trong tam giác SAD)
Lại có MN // BS và SB ∩ SA = S
Do đó MN không thể song song với PQ
Xét tứ giác MNPQ có NP // MQ (//CD)
Do đó MNPQ là hình thang.
Vậy khẳng địn (1) và (3) đúng.
Đáp án B

1: Xét ΔABC có BM/BA=BN/BC=1/2
nên MN//AC và MN=1/2AC
Xét ΔADC có DP/DC=DQ/DA
nên QP//AC và QP/AC=DP/DC=1/2
=>QP=1/2AC
=>MN//PQ và MN=PQ
Xét ΔABD có AM/AB=AQ/AD=1/2
nên MQ/BD=AM/AB=1/2
=>MQ=1/2BD
Xét ΔCBD có CP/CD=CN/CB=1/2
nên NP=1/2BD
=>MQ=NP=1/2BD
mà BD=AC
nên MQ=NP=QP=MN
2: Xét tứ giác MNPQ có
MN//PQ
MN=PQ
MN=MQ
=>MNPQ là hình thoi

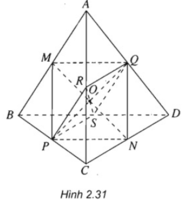
Trong tam giác ABC ta có:
MP // AC và MP = AC/2.
Trong tam giác ACD ta có:
QN // AC và QN = AC/2.
Từ đó suy ra {MP // QN}
⇒ Tứ giác MNPQ là hình bình hành.
Do vậy hai đường chéo MN và PQ cắt nhau tại trung điểm O của mỗi đường.
Tương tự: PR // QS và PR = QS = AB/2. Do đó tứ giác PQRS là hình bình hành.
Suy ra hai đường chéo RS và PQ cắt nhau tại trung điểm O của PQ và OR = OS
Vậy ba đoạn thẳng MN, PQ và RS cắt nhau tại trung điểm mỗi đoạn.
Vì M,N lần lượt là trung điiểm của AB và AC (tgt)
=> MN // BC và MN = 1/2 BC (t/c)đường TB của tam giác)(1)
Vì P,Q l3 trung điểm của CD và BD
=> PQ//BC và PQ=1/2 BC (t/c đg Tb ...)(2)
Từ (1)và(2) => MN//PQ và MN = PQ
=> MNPQ là hbh