Cho hình lăng trụ đứng có diện tích xung quanh là 288. Chu vi đáy 240. Chiều cao của hình lăng trụ đứng là: *
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 5 2019
a. Thể tích là:
\(\frac{3x4}{2}\)x 9 = 54 cm3
Trong tam giác vuông ABC (vuông tại A), theo định lý Pytago, ta có cạnh huyền bằng:
\(\sqrt{3^2+4^2}\) = 5 cm
Diện tích xung quanh là:
(3 + 4 + 5) x 9 = 108 cm2
Diện tích toàn phần là:
108 + 3 x 4 = 120 cm2
5 tháng 5 2019
b. Diện tích xung quanh là:
(3 + 4) x 2 x 5 = 70 cm2
Đáp số : 70 cm2
CM
27 tháng 7 2019
Do đáy của hình lăng trụ là lục giác đều cạnh 6cm nên chu vi đáy là:
P = 6.6 = 36cm
Diện tích xung quanh của hình lăng trụ là:
S x q = P . h = 36 . 6 = 216 c m 2
Chọn đáp án B
HN
1
26 tháng 5 2022
bán kính đáy của đáy là:
16 : 3,14 : 2 = 2,5477707 (cm)
diện tích đáy là:
(2,5477707)2 x 3,14 = 20,38216559 (cm2)
chiều cao là:
128 : 20,38216559 = 6,28 (cm)
23 tháng 4 2023
Gọi chiều cao h và cạnh đáy của hình lăng trụ đứng là a, ta có: Diện tích xung quanh của hình lăng trụ đứng là 120cm2 => Chu vi đáy của hình lăng trụ đứng là P = 120 : h Vì đáy của hình lăng trụ là tam giác đều nên có thể tính diện tích đáy bằng công thức: S = (a2 * √3) / 4 Vậy diện tích xung quanh của hình lăng trụ đều bằng: 120 = P * h = (a * √3) / 4 * h => a = 8√5 và h = 15√3 Vậy chiều cao của hình lăng trụ đứng đó là 15√3, độ dài cạnh đáy của hình lăng trụ là 8√5.
23 tháng 4 2023
S xq=120cm2
=>h*3a=120cm2
=>h*a=40cm2
=>\(\left(h,a\right)\in\left\{\left(1;40\right);\left(2;20\right);\left(4;10\right);\left(5;8\right);\left(8;5\right);\left(10;4\right);\left(20;2\right);\left(40;1\right)\right\}\)
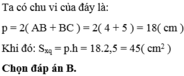
Sxq= 2p.h
=> 288=240.h
=> hh=1.2
Vậy chiều cao của hình lăng trụ là 1,2