chứng minh các số sau đều là số chính phương
a,a=n2+10.n+25
b,b=16.n2+8.n+1
c,c=9.n2+12.n+4
d,d=n.(n+1).(n+2).(n+3)+1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left(2-n\right)\left(n^2-3n+1\right)+n\left(n^2+12\right)+8\)
\(=2n^2-6n+2-n^3+3n^2-n+n^3+12n+8\)
\(=5n^2+5n+10\)
\(=5\left(n^2+n+2\right)⋮5\) (đpcm)


Ta có với mọi số nguyên m thì m2 chia cho 5 dư 0 , 1 hoặc 4.
+ Nếu n2 chia cho 5 dư 1 thì n 2 = 5 k + 1 = > n 2 + 4 = 5 k + 5 ⋮ 5 ; k ∈ N * .
Nên n2+4 không là số nguyên tố
+ Nếu n2 chia cho 5 dư 4 thì n 2 = 5 k + 4 = > n 2 + 16 = 5 k + 20 ⋮ 5 ; k ∈ N * .
Nên n2+16 không là số nguyên tố.
Vậy n2 ⋮ 5 hay n ⋮ 5

Ta có:
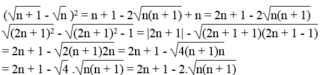
Vế trái bằng vế phải nên đẳng thức được chứng minh.
* Với n = 1, ta có: 2 - 1 2 = 9 - 8
* Với n = 2, ta có: 3 - 2 2 = 25 - 24
* Với n = 3, ta có: 4 - 3 2 = 49 - 48
* Với n = 4, ta có: 5 - 4 2 = 81 - 80


đặt 2n + 34 = a^2
34 = a^2-n^2
34=(a-n)(a+n)
a-n thuộc ước của 34 là { 1; 2; 17; 34} và a-n . Ta có bảng sau ( mik ko bt vẽ)
=> a-n 1 2
a+n 34 17
Mà tổng và hiệu 2 số nguyên cùng tính chẵn lẻ
Vậy ....
Ta cóS = 14 +24 +34 +···+1004 không là số chính phương.
=> S= (1004+14).100:2=50 900 ko là SCP
a, Ta có
a=n2+10n+25
=n2+5n+5n+25
=n(n+5)+5(n+5)
=(n+5)2
bTa có
b=16n2+4n+4n+1
=4n(4n+1)+(4n+1)
=(4n+1)2
c,
c=9n2+12n+4
=(3n)2+6n+6n+22
=3n(3n+2)+2(3n+2)
=(3n+2)2
d,
n.(n+1)(n+2)(n+3)+1
=n(n+3)(n+1)(n+2)+1
=(n2+3n)(n2+3n+2)+1
Đặt n2+3n+1=x
=>(n2+3n)(n2+3n+2)+1=(x-1)(x+1)+1
=(x2+x-z-1)+1
=x2=(n2+3n+1)2
Cảm ơn bạn