c/m tính chất đồng biến nghịch biến của hàm số y= ax2 trong các trường hợp sau
TH1: nếu a>0 => đồng biến khi x thuộc R+
TH2: nếu a<0 => nghịch biến khi x thuộc R+
TH3: nếu a<0 => đồng biến khi x thuộc R-
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
22 tháng 10 2017
Vẽ hình:
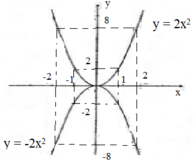
a) Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0
Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.
Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị bào của x để hàm số đạt giá trị nhỏ nhất.
b) Đồ thị hàm số y = a x 2 là đường cong (đặt tên là parabol) đi qua gốc tọa độ nhận trục tung Oy làm trục đối xứng.
Nếu a > 0 thì đồ thị nằm trên trục hoành, điểm O là điểm thấp nhất đồ thị (gọi là đỉnh parabol).
Nếu a < 0 thì đồ thị nằm bên dưới trục hoành, điểm O là điểm cao nhất của đồ thị.
CM
28 tháng 6 2017
Vẽ hình:
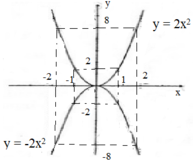
Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0
Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.
Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị bào của x để hàm số đạt giá trị nhỏ nhất.
CM
27 tháng 5 2018
Đáp án A
Phương pháp:
Xét tính đúng sai của các đáp án dựa vào các kiến thức hàm số đồng biến, nghịch biến trên khoảng xác định.
Cách giải:
*2 sai vì với c 1 < c 2 bất kỳ nằm trong a ; b ta chưa thể so sánh được f c 1 và f c 2
*3 sai. Vì y' bằng 0 tại điểm đó thì chưa chắc đã đổi dấu qua điểm đó. VD hàm số y = x 3
*4 sai: Vì thiếu điều kiện tại f ' x = 0 hữu hạn điểm.VD hàm số y = 1999 có y ' = 0 ≥ 0 nhưng là hàm hằng.
Chú ý khi giải:
HS thường nhầm lẫn:
- Khẳng định số 4 vì không chú ý đến điều kiện bằng 0 tại hữu hạn điểm.
- Khẳng định số 3 vì không chú ý đến điều kiện đổi dấu qua nghiệm.
17 tháng 8 2021
a: Khi x>0 thì y>0
=> Hàm số đồng biến
Khi x<0 thì y<0
=> Hàm số nghịch biến
b: Khi x>0 thì y<0
=> Hàm số nghịch biến
Khi x<0 thì y<0
=> Hàm số đồng biến
CM
12 tháng 11 2017
a) Ta có a = 1- √5 < 0 nên hàm số đã cho nghịch biến trên R.
b) Khi x = 1 + √5 ta có:
y = (1 - √5).(1 + √5) - 1 = (1 - 5) - 1 = -5
c) Khi y = √5 ta có:
√5 = (1 - √5)x - 1
=> √5 + 1 = (1 - √5)x
(hoặc trục căn thức ở mẫu như dưới đây:
2 tháng 6 2022
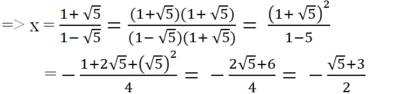
a: Để hàm số đồng biến thì m-1>0
hay m>1
Để hàm số nghịch biến thì m-1<0
hay m<1
b: f(1)=2
nên \(m-1+2m-3=2\)
=>3m-4=2
hay m=2
Do đó: \(f\left(x\right)=x+1\)
f(2)=3
c: f(3)=0 nên 3(m-1)+2m-3=0
=>3m-3+2m-3=0
=>5m=6
hay m=6/5
Vậy: \(f\left(x\right)=\dfrac{1}{5}x-\dfrac{3}{5}\)
=>f(x) đồng biến
19 tháng 2 2022
Bài 1:
a: Để hàm số đồng biến khi x>0 thì m-1>0
hay m>1
b: Để hàm số nghịch biến khi x>0 thì 3-m<0
=>m>3
c: Để hàm số nghịch biến khi x>0 thì m(m-1)<0
hay 0<m<1
19 tháng 2 2022
a, đồng biến khi m - 1 > 0 <=> m > 1
b, nghịch biến khi 3 - m < 0 <=> m > 3
c, nghịch biến khi m^2 - m < 0 <=> m(m-1) < 0
Ta có m - 1 < m
\(\left\{{}\begin{matrix}m-1< 0\\m>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< 1\\m>0\end{matrix}\right.\Leftrightarrow0< m< 1\)
TH1: Lấy \(x_1;x_2\in R\) sao cho \(0< x_1< x_2\)
\(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{a\cdot\left(x_1^2-x_2^2\right)}{x_1-x_2}=a\cdot\left(x_1+x_2\right)\)>0 vì \(x_1+x_2>0;a>0\)
=>Hàm số y=f(x)=ax2 đồng biến khi x>0 nếu a>0
TH2: Lấy \(x_1;x_2\in R^+;0< x_1< x_2\)
\(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{a\cdot\left(x_1^2-x_2^2\right)}{x_1-x_2}=\dfrac{a\left(x_1-x_2\right)\left(x_1+x_2\right)}{x_1-x_2}\)
\(=a\left(x_1+x_2\right)< 0\)(vì x1+x2>0 và a<0)
=>Hàm số nghịch biến khi x>0
TH3: Lấy \(x_1;x_2\in R^-\) sao cho \(x_1< x_2< 0\)
\(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{a\left(x_1^2-x_2^2\right)}{x_1-x_2}=\dfrac{a\left(x_1+x_2\right)\left(x_1-x_2\right)}{x_1-x_2}\)
\(=a\left(x_1+x_2\right)>0\) vì a<0 và x1+x2<0
=>Hàm số đồng biến khi x<0