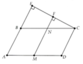
Cho tam giác ABC nhọn có trực tâm H. Các đường vuông góc với AB tại B và vuông góc với AC tại C cắt nhau tại D.
5, Tìm điều kiện của tam giác để tứ giác BDCH là hình vuông
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.






a: Ta có:BD\(\perp\)AB
CH\(\perp\)AB
Do đó: BD//CH
Ta có: CD\(\perp\)CA
BH\(\perp\)CA
Do đó: CD//BH
Xét tứ giác BHCD có
BH//CD
BD//CH
Do đó: BHCD là hình bình hành
b: ta có: BHCD là hình bình hành
=>BC cắt HD tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của HD
=>H,M,D thẳng hàng
d: Để hình bình hành BHCD trở thành hình thoi thì HB=HC
=>ΔHBC cân tại H
=>\(\widehat{HBC}=\widehat{HCB}\)
Ta có: \(\widehat{HBC}+\widehat{ACB}=90^0\)(BH\(\perp\)AC)
\(\widehat{HCB}+\widehat{ABC}=90^0\)(CH\(\perp\)AB)
mà \(\widehat{HBC}=\widehat{HCB}\)
nên \(\widehat{ABC}=\widehat{ACB}\)

\(a,\) Vì H là trực tâm nên BH,CH là đường cao tam giác ABC
\(\Rightarrow BH\perp AC;CH\perp AB\\ \Rightarrow BH\text{//}CD;CH\text{//}BD\\ \Rightarrow BDCH\text{ là hbh}\)
\(b,BDCH\text{ là hbh}\Rightarrow\widehat{BHC}=\widehat{BDC}\\ \text{Xét tứ giác }ABCD:\widehat{BAC}+\widehat{BAD}+\widehat{DAC}+\widehat{BDC}=360^0\\ \Rightarrow\widehat{BAC}+\widehat{BDC}=360^0-90^0-90^0=180^0\\ \Rightarrow\widehat{BAC}+\widehat{BHC}=180^0\)
\(c,\) Gọi O là trung điểm AD \(\Rightarrow OA=OD=\dfrac{1}{2}AD\)
\(\Delta ABD\text{ và }\Delta ACD\text{ vuông tại }B,C\text{ có }BO,CO\text{ là trung tuyến ứng ch }AD\)
\(\Rightarrow BO=CO=\dfrac{1}{2}AD\)
Vậy \(AO=BO=CO=DO\) hay A,B,C,D cách đều O

Xét tứ giác BDCH có
BD//CH
BH//CD
Do đó: BDCH là hình bình hành

Xet tam giác ABC có H là trực tâm nên\(\hept{\begin{cases}CH\perp AB\\BH\perp AC\end{cases}}\)
Ta có \(\hept{\begin{cases}DB\perp AB\left(gt\right)\\CH\perp AB\left(cmt\right)\end{cases}\Rightarrow D}B//CH\)
\(\hept{\begin{cases}DC\perp AC\left(gt\right)\\BH\perp AC\left(cmt\right)\end{cases}\Rightarrow DC//BH}\)
Xét tứ giác BDCH có DB//CH (cmt) vầ DC//BH (cmt) nên tứ giác BDCH là hbh ( théo dấu hiệu nhận biết hbh) đpcm

a) Vì BHCD có các cặp cạnh đối song song nên là hình bình hành.
b) Tứ giác ABCD có A B D ^ = A C D ^ = 90 0 m à B A C ^ = 60 0 nên B D C ^ = 120 0

a)BH vuông góc với AC
CD vuông góc với AC =>BH//CD
Tương tự HC//BD =>BDCH là HBH
b)góc BDC=góc BHC
HC cắt AB tại E => góc AEH=900
HB cắt AC tại F => góc AFH=900
=>góc EHF=góc BHC= góc BDC
góc AEH+góc AFH+góc EHF+góc ABC =3600
=>góc BDC+góc ABC=1800

a)BH vuông góc với AC
CD vuông góc với AC =>BH//CD
Tương tự HC//BD =>BDCH là HBH
b)góc BDC=góc BHC
HC cắt AB tại E => góc AEH=900
HB cắt AC tại F => góc AFH=900
=>góc EHF=góc BHC= góc BDC
góc AEH+góc AFH+góc EHF+góc ABC =3600
=>góc BDC+góc ABC=1800