1 tàu chở hàng đi từ cảng A đến cảng B câch nhau 900km với vận tốc không đổi là x(km/h).Khi đi được 1/3 quãng đừơng thì một động cơ của tàu bị hỏng nên tàu chỉ cond chạy với vận tốc 12(km/h) trong suốt 3 giờ tàu sửa chữa động cơ. Để về cảng B không muộn hơn dự định,tàu phải tăng vận tốc thêm 5km/h . Viết phân thức tính thời gian thực tế để tàu đi từ cảng A đến cảng B
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
a) Ta có sơ đồ đường đi như sau:
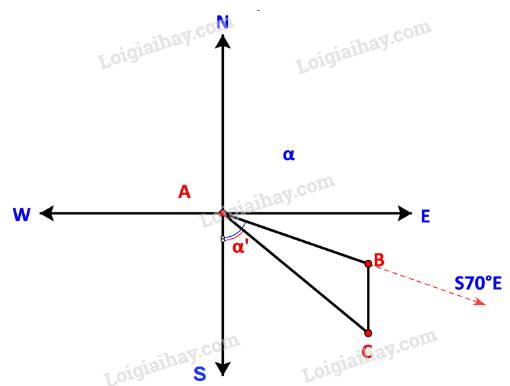
Trong đó: B là nơi động cơ bị hỏng, C là ví trí neo đậu của tàu trên hòn đảo.
Khoảng cách từ cảng A tới đảo nơi tàu neo đậu là đoạn AC.
Quãng đường tàu đi được sau 90 phút hay 1,5 giờ (ngay trước khi hỏng động cơ) là:
70.1,5 = 105 (km) hay AB = 105.
Sau 2 giờ tàu trôi tự do từ B đến C với vận tốc 8km/h , suy ra BC= 8.2 = 16 (km).
Ban đầu tàu di chuyển theo hướng \(S{70^o}E\) nên \(\widehat {BAS} = {70^o}\). Sau khi động cơ bị hỏng, tàu trôi theo hướng Nam do đó BC song song với AS.
\( \Rightarrow \widehat {ABC} = {180^o} - \widehat {BAS} = {110^o}\)
Áp dụng định lí cosin cho tam giác ABC ta có:
\({AC^2} = {BC^2} + {AB^2} - 2.AC.BC.\cos B\)
\(\begin{array}{l} \Rightarrow {AC^2} = {16^2} + {105^2} - 2.16.105.\cos {110^o} \approx 12430\\ \Rightarrow AC \approx 111,5.\end{array}\)
Vậy khoảng cách từ cảng A tới đảo nơi tàu neo đậu là khoảng 111,5 km.
b)
Theo sơ đồ, hướng từ cảng A tới đảo nơi tàu neo đậu là \(S{\alpha ^o}E\) với \({\alpha ^o} = \widehat {CAS}\).
Do BC // AS nên \(\widehat {CAS}= \widehat {ACB}\)
Áp dụng định lí sin cho tam giác ABC ta có:
\(\frac{BC}{{\sin A}} = \frac{AC}{{\sin B}} = \frac{AB}{{\sin C}}\)\( \Rightarrow \sin C = \frac{{AB.\sin B}}{AC}\)
Mà \(\widehat B = {110^o}\); \(AC \approx 111,5\); AB = 105.
\(\begin{array}{l} \Rightarrow \sin C= \frac{{105.\sin {{110}^o}}}{{111,5}} \approx 0,885\\ \Rightarrow \widehat C \approx {62^o}(do\;\widehat C < {90^o})\end{array}\)
Vậy hướng từ cảng A tới đảo nơi tàu neo đậu là \(S{62^o}E\).

Đáp án D.
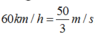
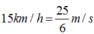
Sử dụng công thức
![]()
Giai đoạn tàu chuyển động từ vận tốc 60 km/h giảm xuống còn 15 km/h:
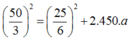
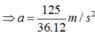
Gia đoạn tàu chuyển động từ 15 km/h tới khi dừng lại hẳn:
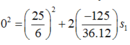
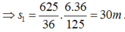
.

Gọi vận tốc của tàu trở hàng là v (km/h) => vận tốc tàu trở khách là v + 7 (km/h)
Vì tàu trở hàng đi được 1,5h thì tàu trở khách mới xuất phát nên khi tàu trở khách đi đc 4h thì tàu trở hàng đi được 5,5h
Quãng đường tàu trở hàng đi đc sau 5,5h là : 5,5v (km)
Quãng đường tàu trở khách đi đc sau 4h là : 4(v + 7) (km)
Do sau 4h tàu trở khách cách tàu trở hàng 45 km nên ta có phương trình :
\(S_{AB}-5,5v-4\left(v+7\right)=45\)
\(\Leftrightarrow319-5,5v-4v-28=45\)
\(\Leftrightarrow291-9,5v=45\)
\(\Rightarrow v=\frac{291-45}{9,5}=\frac{492}{19}\approx26\left(\frac{km}{h}\right)\) \(\Rightarrow v+7\approx33\left(\frac{km}{h}\right)\)
Vậy vận tốc của tàu trở hàng là 26 (km/h) => vận tốc tàu trở khách là 33 (km/h)
https://h.vn/hoi-dap/question/261561.html
đây là bài dự phòng nếu em đánh sai 25 thành 45 nhá

Gọi x (km/h) là vận tốc của tàu hàng. Điều kiện: x > 0
Vận tốc của tàu khách là x + 7 (km/h)
Thời gian tàu hàng từ lúc đi đến lúc cách tàu khách 25km là:
1,5 + 4 = 5,5 (giờ)
Quãng đường tàu hàng đi được trong 5,5 giờ là 5,5x (km)
Quãng đường tàu khách đi được trong 4 giờ là 4(x + 7) (km)
Theo đề bài ta có phương trình:
5,5x+4(x+7)=319−25⇔5,5x+4x+28=294⇔9,5x=294−28⇔9,5x=2665,5x+4(x+7)=319−25⇔5,5x+4x+28=294
⇔9,5x=294−28⇔9,5x=266
(thỏa)
Gọi x (km/h) là vận tốc của tàu hàng. Điều kiện: x > 0 Vận tốc của tàu khách là x + 7 (km/h) Thời gian tàu hàng từ lúc đi đến lúc cách tàu khách 25km là: 1,5 + 4 = 5,5 (giờ) Quãng đường tàu hàng đi được trong 5,5 giờ là 5,5x (km) Quãng đường tàu khách đi được trong 4 giờ là 4(x + 7) (km) Theo đề bài ta có phương trình: 5,5x+4(x+7)=319−25⇔5,5x+4x+28=294⇔9,5x=294−28⇔9,5x=2665,5x+4(x+7)=319−25⇔5,5x+4x+28=294 ⇔9,5x=294−28⇔9,5x=266

Gọi x (km/h) là vận tốc của tàu hàng. Điều kiện: x > 0
Vận tốc của tàu khách là x + 7 (km/h)
Thời gian tàu hàng từ lúc đi đến lúc cách tàu khách 25km là:
1,5 + 4 = 5,5 (giờ)
Quảng đường tàu hàng di được trong 5,5 giờ là 5,5x (km)
Quãng dường tàu khách đi được trong 4 giờ là 4(x + 7) (km)
Theo đề bài ta có phương trình:
5,5x + 4(x + 7) = 319 - 25 ⇔ 5,5x + 4x + 28 = 294
⇔ 9,5x = 294 - 28 ⇔ 9,5x = 266 ⇔ x = 28 (thỏa)
Vậy vận tốc của tàu hàng là 28 km/h.
Vận tốc của tàu khách là 28 + 7 = 35 km/h.

1/3 quãng đường dài: \(900\cdot\dfrac{1}{3}=300\left(km\right)\)
Thời gian để xe đi hết 300km đầu là: \(\dfrac{300}{x}\left(h\right)\)
Độ dài quãng đường xe chạy trong 3 giờ tiếp theo là: \(12\cdot3=36\left(km\right)\)
Độ dài quãng đường còn lại là: 900-300-36=600-36=564(km)
Thời gian xe đi hết quãng đường còn lại là:
\(\dfrac{564}{x+5}\left(h\right)\)
Thời gian dự kiến ban đầu là \(\dfrac{900}{x}\left(giờ\right)\)
Thời gian thực tế tàu đi từ cảng A đến cảng B là:
\(\dfrac{300}{x}+3+\dfrac{564}{x+5}\)(h)