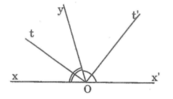
Cho góc xOy và góc yOx' là 2 góc kề bù. Gọi Ot và Ot' lần lượt là phân giác của góc xOy và góc yOx'. Chứng minh Ot vuông góc Ot'
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 9 2018
ta có: Ot là tia phân giác góc xOy
=> góc tOy = góc xOy/2
=> góc xOy = 2. góc tOy
ta có: Ot' là tia phân giác góc yOx'
=> góc yOt' = góc yOx'/2
=> góc yOx' = góc yOt'.2
ta có: góc xOy và góc yOx' kề bù
=> góc xOy + góc yOx' = 180 độ
=> góc tOy.2 + góc góc yOt'.2 = 180 độ
2. ( góc tOy + góc yOt') = 180 độ
=> góc tOy + góc yOt' = 90 độ
=> góc tOt' = 90 độ
\(\Rightarrow Ot\perp Ot'\) ( định lí)
b tự kẻ hình nha
14 tháng 6 2015
Ta có: ot là tia phân giác của góc xoy => toy = xoy/2
ot' là tia phân giác của góc zoy => t'oy = zoy/2
Suy ra, toy + t'oy = xoy/2 + zoy/2
tot' = (xoy+zoy)/2
Vì xoy và zoy kề bù nên xoy+zoy=180o
=> tot' = 180o/2
tot' = 90o
Vậy ot vuông góc với ot'
5 tháng 9 2018
Vì Ot là tia phân giác của xOy => tOy = 1/2 . xOy
Vì Ot' là tia phân giác của yOx' => yOt' = 1/2 . yOx'
=> tOy + yOt' = 1/2 . xOy + 1/2 . yOx'
=> tOt' = 1/2 ( xOy + yOx' )
=> tOt' = 1/2 . 180độ ( kề bù )
=> tOt' = 90độ
=> Ot vuông góc với Ot' ( đpcm )
23 tháng 7 2018
I don't now
...............
.................