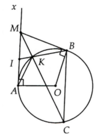
Cho A nằm trên (O). Vẽ tiếp tuyến Ax với (O). Lấy M nằm trên Ax. vẽ tếp tuyến MB với (O) tại B. Gọi I là trung điểm MA, BI cắt (O) tại K
a) c/m tam giác IKA đồng dạng IAB
b) MK cắt (O) tại C. c/m BC//MA
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
29 tháng 7 2018
a, ∆IAK:∆IBA => I A I B = I K I A
Mà IA = IM => I M I B = I K I M
=> ∆IKM:∆IMB
b, Chứng minh được: I M K ^ = K C B ^ => BC//MA(đpcm)
22 tháng 12 2021
1: Xét (O) có
CM là tiếp tuyến
CA là tiếp tuyến
Do đó: CM=CA
Xét (O) có
DM là tiếp tuyến
DB là tiếp tuyến
Do đó: DM=DB
Ta có: CM+DM=CD
nên CD=AC+BD
21 tháng 6 2023
a: Xét ΔMAO và ΔMCO có
MA=MC
AO=CO
MO chung
=>ΔMAO=ΔMCO
=>góc MCO=90 độ
góc MAO+góc MCO=180 độ
=>MAOC nội tiếp đường tròn đường kính MO
=>I là trung điểm của MO
b: góc MCO=90 độ
=>MC là tiếp tuyến của (O)
Xét ΔMCD và ΔMBC có
góc MCD=góc MBC
góc CMD chung
=>ΔMCD đồng dạng với ΔMBC
=>MC/MB=MD/MC
=>MC^2=MB*MD
6 tháng 1 2022
a: Xét (O) có
ΔABC nội tiếp
AB là đường kính
Do đó: ΔABC vuông tại C
Xét ΔACB vuông tại C có
\(\sin\widehat{CBA}=\dfrac{CA}{AB}=\dfrac{1}{2}\)
=>CA=R
hay \(CB=R\sqrt{3}\)
b: Xét ΔMAB vuông tại A có AC là đường cao
nên \(BC\cdot MC=AC^2\left(1\right)\)
Xét ΔACB vuông tại C có CH là đường cao
nên \(AH\cdot AB=AC^2\left(2\right)\)
Từ (1) và (2) suy ra \(MC\cdot BC=AH\cdot AB\)
a: Xét (O) có
\(\widehat{IAK}\) là góc tạo bởi tiếp tuyến AI và dây cung AK
\(\widehat{IBA}\) là góc nội tiếp chắn cung AK
Do đó: \(\widehat{IAK}=\widehat{IBA}\)
Xét ΔIAK và ΔIBA có
\(\widehat{IAK}=\widehat{IBA}\)
\(\widehat{AIK}\) chung
Do đó: ΔIAK đồng dạng với ΔIBA