1, Cho tam giác DEF vuông tại D. M là trung điểm EF kẻ MI vuông góc DE, MK vuông góc DF a, Tứ giác DIMK là hình chữ nhật b, Trên tia đối MD lấy H: MD=MH. Chứng minh DEHF là hình chữ nhật
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a/ Xét tứ giác DPMQ có
∠EDF=∠MQD=ˆMPD=90oEDF^=MQD^=MPD^=90o
=> Tứ giác DPMQ là hcn
b/ Để hcn DPMQ là hình vuông thì DM là tia pg ^EDF
c/ Có I đx M qua DE
=> DE là đường t/trực của IM
=> DI = DM (1)
=> t/g DIM cân tại D có DE là đường trung trực
=> DE đồng thời là đường pg
=> ˆIDE=ˆEDMIDE^=EDM^ (2)
CMTT : DM = DK (3) ; ˆKDF=ˆFDMKDF^=FDM^ (4)
Từ (2) ; (4)
=> ∠IDE+∠EDF+∠KDF=∠IDK=180oIDE^+EDF^+KDF^=IDK^=180o
=> I,D,K thẳng hàng
Từ (1) ; (3)=> ID = DK
Do đó D là trđ IK
=> I đx K qua D

a: Xét tứ giác AHCD có
M là trung điểm chung của AC và HD
góc AHC=90 độ
=>AHCD là hình chữ nhật
b: Xét tứ giác ADHE có
AD//HE
AD=HE
=>ADHE là hình bình hành

a: Xét tứ giác AMHN có
\(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)
Do đó: AMHN là hình chữ nhật
b: Xét ΔABC có
H là trung điểm của BC
HN//AB
Do đó: N là trung điểm của AC
Xét ΔABC có
H là trung điểm của BC
HM//AC
Do đó: M là trung điểm của AB
Xét tứ giác AHBP có
M là trung điểm chung của AB và HP
=>AHBP là hình bình hành
Hình bình hành AHBP có AB\(\perp\)HP
nên AHBP là hình thoi
Để AHBP là hình vuông thì \(\widehat{HBP}=90^0\)
AHBP là hình thoi nên BA là phân giác của góc HBP
=>\(\widehat{HBA}=\dfrac{1}{2}\cdot\widehat{HBP}=45^0\)
=>\(\widehat{ABC}=45^0\)

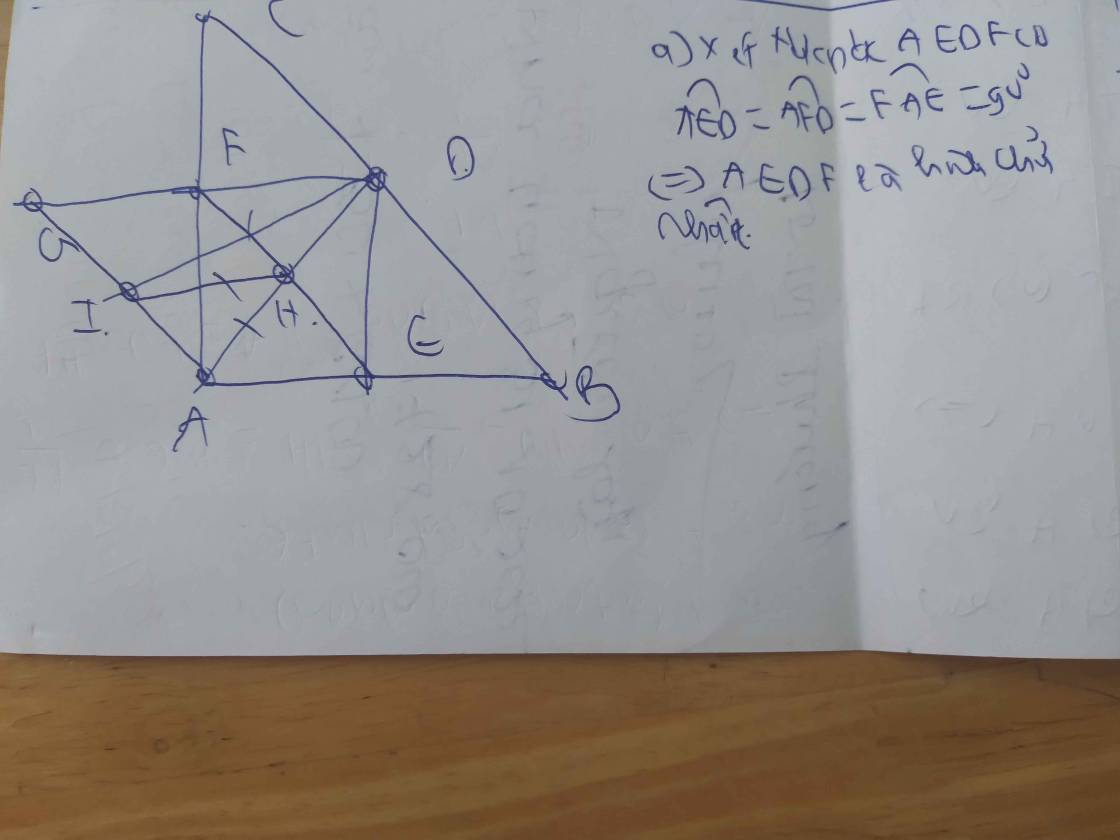
a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật
b: Xét ΔABC có
D là trung điểm của BC
DE//AC
Do đó: E là trung điểm của AB
Xét ΔABC có
D là trung điểm của BC
DF//AB
Do đó: F là trung điểm của AC
FG=FD
G,F,D thẳng hàng
Do đó: F là trung điểm của GD
Xét tứ giác ADCG có
F là trung điểm chung của AC và GD
=>ADCG là hình bình hành
Hình bình hành ADCG có AC\(\perp\)GD
nên ADCG là hình thoi

\(a,\) Vì M là trung điểm AB cà DH nên AHBD là hình bình hành
Mà \(\widehat{AHB}=90^0\) (đường cao AH) nên AHBD là hcn
\(b,\) Vì AHBD là hcn nên \(AD=BH;AD\text{//}HB\)
Mà \(BH=HE\Rightarrow AD=HE;AD\text{//}HE\)
Do đó: ADHE là hình bình hành
\(c,\) Vì ADHE là hbh mà N là giao AH và DE nên N là trung điểm AH và DE
Mà M là trung điểm AB nên MN là đtb \(\Delta ABH\)
Do đó \(MN//BH\) hay \(MN//BC\)
Ta có N là trung điểm AH và K là trung điểm AC nên NK là đtb \(\Delta ACH\)
Do đó \(NK//HC\) hay \(NK//BC\)
Do đó theo định lí Ta lét thì MN trùng NK hay M,N,K thẳng hàng
a: Xét tứ giác AHBD có
M là trung điểm của AB
M là trung điểm của HD
Do đó: AHBD là hình bình hành
mà \(\widehat{AHB}=90^0\)
nên AHBD là hình chữ nhật

a) Xét △DEM và △KFM có
DM=KM(giả thiết)
góc DME=góc KMF(2 góc đối đỉnh)
EM=MF(Vì M là trung điểm của EF)
=>△DEM =△KFM(c-g-c)
=> góc MDE=góc MKF (2 góc tương ứng)
hay góc EDK= góc EKD mà 2 góc này là 2 góc so le trong bằng nhau của đường thẳng DK cắt 2 đường thẳng DE và KF
=>DE//KF
b) ta có DH⊥EF hay DP⊥EF => góc DHE =góc PHE =90 độ
Xét △DHE (góc DHE=90 độ)△PHE(góc PHE=90 độ) có
HD=HP
HE là cạnh chung
=> △DHE= △PHE(2 cạnh góc vuông)
=> góc DEM=góc PEM
=> EH là tia phân giác của góc DEP
hay EF là tia phân giác của góc DEP
vậy EF là tia phân giác của góc DEP



a: Xét tứ giác DIMK có
\(\widehat{DIM}=\widehat{DKM}=\widehat{KDI}=90^0\)
=>DIMK là hình chữ nhật
b: Xét tứ giác DEHF có
M là trung điểm chung của DH và EF
=>DEHF là hình bình hành
Hình bình hành DEHF có \(\widehat{FDE}=90^0\)
nên DEHF là hình chữ nhật
Hình?