Từ công thức 4.2 và 4.3 hãy suy ra công thức...
Đọc tiếp
Từ công thức 4.2 và 4.3 hãy suy ra công thức 4.4
K
Khách
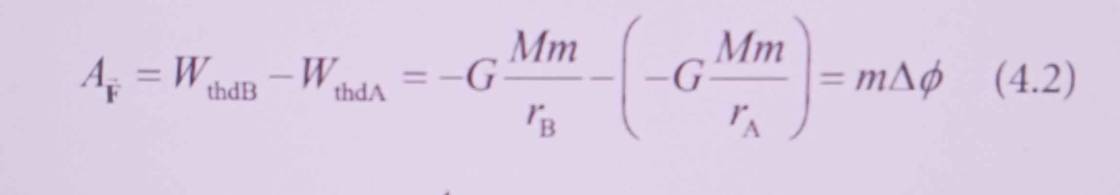
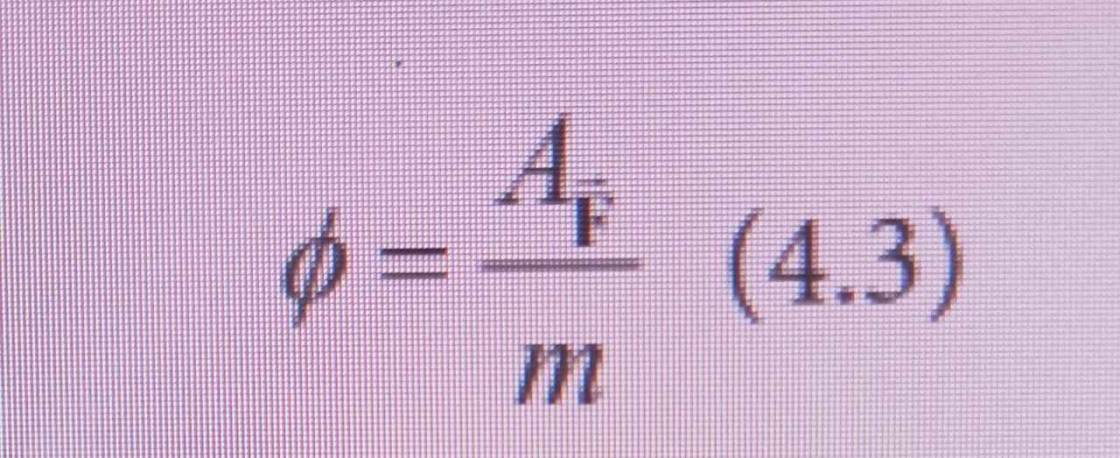
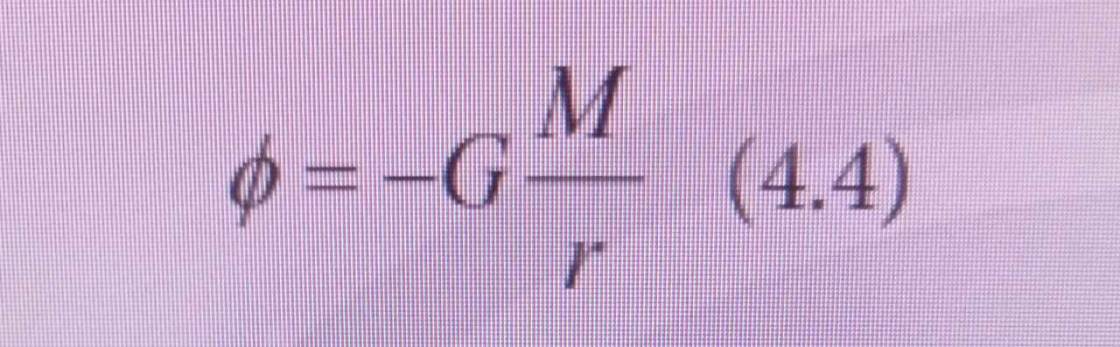
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ND
1
PT
1
CM
5 tháng 11 2017
+) Từ : cos(a - b)= cosa cosb + sina sinb
cos(a + b) = cosa cosb - sina sinb
⇒ cos(a - b) + cos(a + b)= 2cosa cosb
⇒ cosa cosb = 1/2 [cos(a - b) + cos(a + b)]
+) Tương tự: cos(a - b)- cos(a + b) = 2sina sinb
⇒ sinasinb = 1/2 [cos(a - b) - cos(a + b) ]
+) Từ: sin(a - b) = sina cosb - cosa sinb
sin(a + b)= sina cosb + cosa sinb
⇒ sin(a - b) + sin (a + b) = 2 sina cosb
⇒ sina cosb = 1/2 [sin(a - b)+ sin(a + b)]
CM
27 tháng 1 2018
- Diện tích hình vuông cạnh a: S = a2
- Diện tích tam giác vuông có hai cạnh góc vuông a và b là: S = 0,5 ab
HD
1
VT
29 tháng 8 2018
Trong giới hạn đàn hồi, độ biến dạng tỉ đối của vật rắn hình trụ tỉ lệ với ứng suất gây ra nó: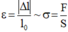 
Có thể viết: 
là hệ số tỉ lệ (E là suất đàn hồi đơn vị là Pa)
Suy ra: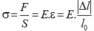 
(E là suất đàn hồi, đơn vị là Pa ; S: Diện tích tiết diện của vật rắn đồng chất, hình trụ. lo: Chiều dài ban đầu của vật).
Chú ý: Với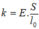 
là hệ số đàn hồi hay độ cứng của thanh rắn, thì lực đàn hồi tính theo biểu thức: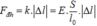 
25 tháng 6 2021
Tham khảo:
a) Tổng số electron là 7, suy ra số thứ tự của nguyên tố là 7. Có 2 lớp electron suy ra nguyên tố ở chu kì 2. Nguyên tố p có 5 electron ở lớp ngoài cùng nên thuộc nhóm VA. Đó là nitơ. Công thức phân tử hợp chất với hidro là NH3.
SG
1
AN
26 tháng 8 2017
Hướng dẫn giải:
Trong giới hạn đàn hổi, độ biến dạng tỉ đối của thanh rắn tỉ lệ thuận với ứng suất của lực kéo thanh đó:
\(\dfrac{\Delta l}{l_0}=\alpha\sigma\)
với α là hệ số tỉ lệ phụ thuộc chấ liệu của thanh rắn.
Lực đàn hồi Fđh tỉ lệ với độ biến dạng ∆l = |l – l0| của thanh rắn:
\(F_{đh}=k\Delta l\) với \(k=E\dfrac{S}{l_0}\)
Trong đó:
\(E=\dfrac{1}{a}=\) suất đàn hồi đặc trưng cho tính đàn hồi của thanh rắn.
Đơn vị của E là paxcan (Pa).
k = độ cứng của thanh rắn phụ thuộc chất liệu và kích thước cuả thanh.
Đơn vị đo của k là N/m
Ta có: Năng lượng thế tại điểm A là: \(W_{thdA}=-G\cdot\dfrac{M\cdot m}{r_A}\)
Và năng lượng thế tại điểm B là: \(W_{thdB}=-G\cdot\dfrac{M\cdot m}{r_B}\)
Hiệu của hai năng lượng thế là:
\(A_{\overrightarrow{F}}=W_{thdB}-W_{thdA}=-G\cdot\dfrac{M\cdot m}{r_B}-\left(-G\cdot\dfrac{M\cdot m}{r_A}\right)=-G\cdot Mm\cdot\left(\dfrac{1}{r_B}-\dfrac{1}{r_A}\right)\)
\(\Rightarrow-G\cdot M\cdot\left(\dfrac{1}{r_B}-\dfrac{1}{r_A}\right)=\dfrac{A_{\overrightarrow{F}}}{m}\left(1\right)\)
Mặt khác: \(\phi=\dfrac{A_{\overrightarrow{F}}}{m}\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) ta suy ra: \(\phi=-G\cdot M\cdot\left(\dfrac{1}{r_B}-\dfrac{1}{r_A}\right)=-G\cdot\dfrac{M}{r}\)