Cho tam giác đều ABC,BC và CE là 2 đường cao cắt nhau tại H
a Chứng minh tam giác BEC=tam giác CDB từ đó suy ra tam giác BHC cân
b Tính góc AED
c Chứng minh BEDC là hình thang cân
d Qua B kẻ đường thẳng vuông góc với AB.Qua C kẻ đường thẳng vuông góc với AC,2 đường này cắt nhau tai I.Chứng minh 3 điểm A,H,I thẳng hàng
Đang cần gấp

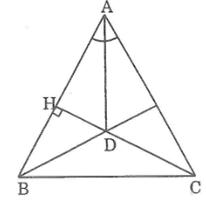
đề bạn ghi sai rồi, phải là BD và CE chứ
a)Tam giác BEC và CDB có:
Góc E=D=90 độ
BC cạnh chung
Góc B=C(tam giác ABC đều)
vậy tam giác BEC=CDB(Cạnh huyền-góc nhọn)
b) Vì tam giác BEC=CDB => BE=CD(cạnh tương ứng)
mà BE+AE=CD+AD
Từ hai điều này suy ra AE=AD. nên tam giác AED cân tại A, lại có góc A bằng 60 độ, nên tam giác AED là tam giác đều
=> Góc AED=60 độ.
c) ta có Góc AED=ABC=60 độ
mà chúng ở vị trí đồng vị nên ED//BC.
Tứ giác BEDC có ED//BC vậy BEDC là hình thang.
Hình thang BEDC có 2 góc kề đáy góc B=C=60 độ
Vậy BEDC là hình thang cân.
d) Xét tam giác ABI và ACI có:
B=C=90 độ
AI cạnh chung
AB=AC
Vậy Tam giác ABI=ACI(Cạnh huyền-cạnh góc vuông)
=>IB=IC hay I thuộc đường trung trực của BC (1)
Tam giác ABC đều, có AH là đường cao nên đồng thời cũng là trung trực của BC (2)
từ (1) và (2) suy ra A, H, I thuộc đường trung trực của BC hay A, H, I thẳng hàng.