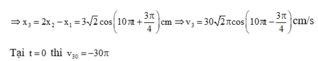Lập trình C++.Lớp 9A có n học sinh, nhà của các học sinh này đều nằm dọc theo con đường tỉnh lộ là một đường thẳng, nhà của học sinh thứ i nằm ở vị trí cách đầu đường là xi (đơn vị độ dài). Vào các ngày nghỉ tết, các học sinh lớp 9A muốn hẹn nhau đến nhà của thành viên trong lớp để liên hoan, vui chơi. Để hạn chế việc đi xa, các bạn muốn chọn nhà của một thành viên trong lớp sao cho tổng khoảng cách mà các học sinh còn lại đến nhà của thành viên được chọn là nhỏ nhất. Yêu cầu: Hãy chọn nhà của một thành viên trong lớp làm địa điểm họp mặt sao cho tổng khoảng cách mà các học sinh còn lại đến nhà của thành viên được chọn là nhỏ nhất. Dữ liệu vào: Cho từ tệp văn bản HOPMAT.INP gồm hai dòng: Dòng thứ nhất ghi số nguyên dương n (2≤n≤106 ). Dòng thứ hai ghi n số nguyên x1, x2, …, xn là khoảng cách từ nhà của mỗi học sinh đến đầu đường, các giá trị xi không trùng nhau (1≤xi≤108 , i=1÷n). Kết quả: Ghi ra tệp văn bản HOPMAT.OUT một số nguyên duy nhất là tổng khoảng cách nhỏ nhất từ nhà của các học sinh lớp 9A đến nhà của học sinh được chọn làm địa điểm họp mặt
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Thời gian đi từ nhà đến trường: 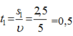 = 30 phút
= 30 phút
Quãng đường học sinh đã đi về trong 10 phút đi là:
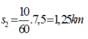
Do đó tốc độ trung bình trong 40 phút:
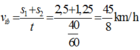

Học sinh nhớ được sau 2 ngày là: \(f\left(2\right)=25\cdot\left(1-e^{-0,2\cdot2}\right)\simeq8\) (đơn vị kiến thức)
Học sinh nhớ được sau 8 ngày là: \(f\left(8\right)=25\cdot\left(1-e^{-0,2\cdot8}\right)\simeq20\) (đơn vị kiến thức)

Đáp án C
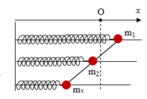
Ta có ω 1 = ω 2 = ω 3 = 10 π rad / s
Phương trình dao động của vật 1 và vật 2 là:
x 1 = 3 cos ( 10 πt - π 2 ) c m x 2 = 1 , 5 cos ( 10 πt ) ( n ế u q u y ư ớ c t ọ a đ ộ x = 1 , 5 = ± A )
Trong quá trình dao động cả ba vật nằm trên một đường thẳng khi 2 x 2 = x 1 + x 3 ⇒ x 3 = 2 x 2 - x 1
tính chất trung bình
Bấm máy tính tổng hợp dao động ta được
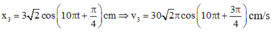
Taị t = 0 và v 30 = - 30 π cm / s
Trường hợp x 2 = 1 , 5 cos ( 10 π t + π ) ( n ế u q u y ư ớ c t ọ a đ ộ x = 1 , 5 = - A )