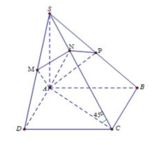
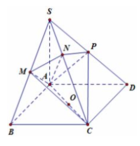
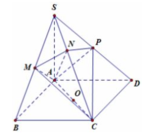
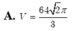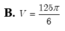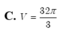. Cho hình chóp S.ABCD với ABCD là hình bình hành điểm M trên cạnh SB, (P) là mặt phẳng qua M và P song song với mp(SAD). a. Tìm giao điểm K của đường thẳng MD với mặt phẳng (SAC) b. Tìm các đoạn giao tuyến của mặt phẳng (P) với các mặt của hình chóp. Hình tạo bởi các đoạn giao tuyến trên là hình gì? Chứng minh. Giúp mình câu b với nha, mình cảm ơn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KB
28 tháng 3 2022
Gọi O là tâm của hình bình hành ABCD; G = SO∩AM ⇒ G là trọng tâm ΔSAC ⇒ SG/SO = 2/3 ⇒ G cũng là trọng tâm ΔSBD
G ∈ AM ⊂ (P); G ∈ SO ⊂ (SBC) (1)
B' ∈ (P) và B' ∈ SB ⊂(SBC) (2)
D' ∈ (P) và D' ∈ SD ⊂(SBC) (3)
Từ (1); (2); (3) ⇒ G; B'; D' ∈ giao tuyến của (P) và (SBC)
Trong (SBC) vẽ BM//SO//DN (M, N ∈ B'D') ⇒ OG là đường trung bình của hình thang BDNM
⇒ BM + DN = 2OG = SG
Ta có :
x = SB/SB' = (SB' + BB')/SB' = 1 + BB'/SB' = 1 + BM/SG
y = SD/SD' = (SD' + DD')/SD' = 1 + DD'/SD' = 1 + DN/SG
⇒ x + y = 2 + (BM + DN)/SG = 2 + 1 = 3
1/x + 1/y = SB'/SB + SD'/SD = a/b
⇒ 3a/b = (x + y)(1/x + 1/y) ≥ 2√(xy).2√(1/xy) = 4
⇒ u = a/b ≥ 4/3 tối giản ⇒ GTNN của u = 4/3 xảy ra khi x = y ⇔ SB'SB' = SD/SD' ⇔ B'D'//BD
11 tháng 10 2021
a: Xét tứ giác EBDA có
EB//DA
EA//DB
Do đó: EBDA là hình bình hành
Xét tứ giác ABDF có
AB//DF
AF//BD
Do đó: ABDF là hình bình hành