kẻ cả hình nx
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
kẻ hình nx nha
24 tháng 12 2023
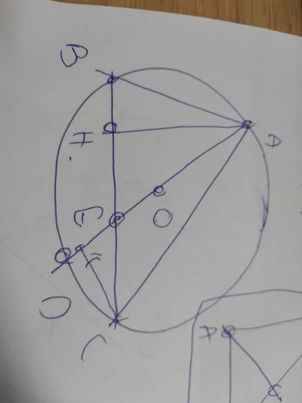
a: Xét tứ giác AHKC có \(\widehat{AHC}=\widehat{AKC}=90^0\)
nên AHKC là tứ giác nội tiếp
=>A,H,K,C cùng thuộc một đường tròn
kẻ hình nx nhé cám ưn nhìu 
7 tháng 12 2023
1: Xét (O) có
ΔAHC nội tiếp
AC là đường kính
Do đó: ΔAHC vuông tại H
=>AH\(\perp\)HC tại H
=>AH\(\perp\)BC tại H
2: Ta có: ΔAHB vuông tại H
mà HM là đường trung tuyến
nên HM=AM=MB
Xét ΔOAM và ΔOHM có
OA=OH
AM=HM
OM chung
Do đó: ΔOAM=ΔOHM
=>\(\widehat{OAM}=\widehat{OHM}=90^0\)
=>MH là tiếp tuyến của (O)
3: Xét (O) có
\(\widehat{DCH}\) là góc nội tiếp chắn cung DH
\(\widehat{DAH}\) là góc nội tiếp chắn cung DH
Do đó; \(\widehat{DCH}=\widehat{DAH}\)
mà \(\widehat{DAH}=\widehat{DAC}\)(AD là phân giác của góc HAC)
nên \(\widehat{DCH}=\widehat{DAC}\)
Xét ΔDCE và ΔDAC có
\(\widehat{DCE}=\widehat{DAC}\)
\(\widehat{CDE}\) chung
Do đó: ΔDCE đồng dạng với ΔDAC
=>\(\dfrac{DC}{DA}=\dfrac{DE}{DC}\)
=>\(DC^2=DA\cdot DE\)
31 tháng 7 2021
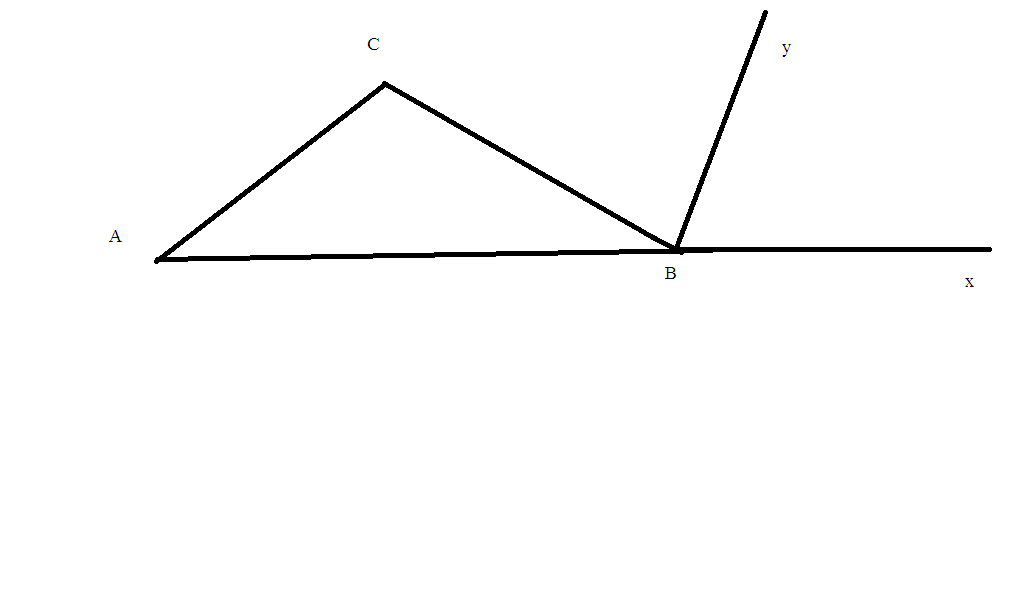
Xét ΔABC có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)(Định lí tổng ba góc của một tam giác)
=>\(100^o+40^o+\widehat{A}=180^O\)
\(\Rightarrow\widehat{A}=40^o\)
a)Xét ΔABC có \(\widehat{xBC}\) là góc ngoài tam giác ABC tại đỉnh B, ta có:
\(\widehat{xBC}=\widehat{C}+\widehat{A}\)
\(\Rightarrow\widehat{xBC}=40^o+100^o=140^o\)
b)Chứng minh // thì đc chứ ⊥ thì, xem lại đề nhé bn
8 tháng 4 2023
a: góc AEB=góc AHB=90 độ
=>ABHE nôi tiếp
b: Gọi N là trung điểm của AB
=>AN=HN=EN=BN
MN là đường trung bình của ΔABC
=>MN//AC
HE vuông góc AC
=>HE vuông góc MN
=>MN là trung trực của HE
=>ME=MH
1 tháng 12 2023
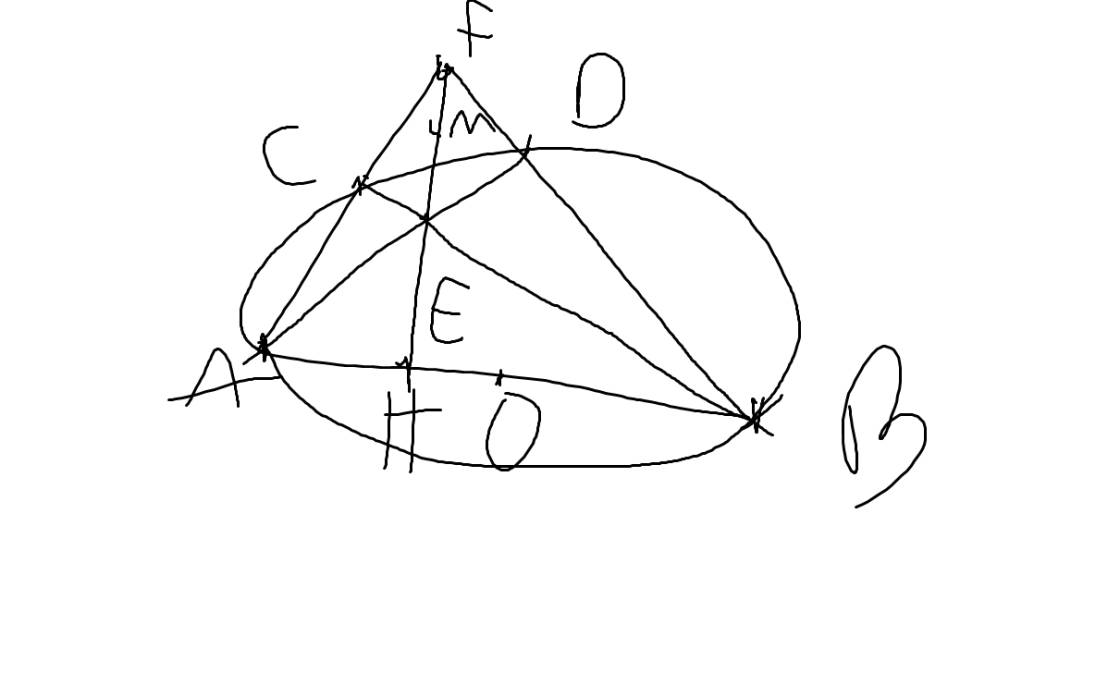
a: Xét (O) có
ΔABC nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>CB\(\perp\)CA tại C
=>CB\(\perp\)AF tại C
Xét tứ giác BHCF có \(\widehat{BHF}=\widehat{BCF}=90^0\)
nên BHCF là tứ giác nội tiếp
=>B,H,C,F cùng thuộc một đường tròn
HA
0
a: Xét (O) có
MA,MC là tiếp tuyến
Do đó: MA=MC
=>M nằm trên đường trung trực của AC(1)
OA=OC
=>O nằm trên đường trung trực của AC(2)
Từ (1) và (2) suy ra MO là đường trung trực của AC
=>MO\(\perp\)AC tại trung điểm của AC
=>MO\(\perp\)AC tại H và H là trung điểm của AC
Xét ΔOAM vuông tại A có AH là đường cao
nên \(OH\cdot OM=OA^2\)
=>\(OH\cdot OM=R^2\)
b: Xét (O) có
ΔADB nội tiếp
AB là đường kính
Do đó:ΔADB vuông tại D
=>AD\(\perp\)DB tại D
=>AD\(\perp\)BM tại D
Xét ΔMAB vuông tại A có AD là đường cao
nên \(BD\cdot BM=BA^2=4R^2\)
c: Xét ΔOAM vuông tại A có AH làđường cao
nên \(AH^2=OH\cdot HM\)
=>\(4\cdot HO\cdot HM=4\cdot AH^2=AC^2\)
d: Xét ΔMAB vuông tại A có AD là đường cao
nên \(MD\cdot MB=MA^2\)
=>\(MD\cdot MB=MC^2\)