Câu 5. (0,75 điểm) Một máy bay cất cánh theo phương có góc nâng $23^\circ$ (so với mặt đất như hình vẽ).
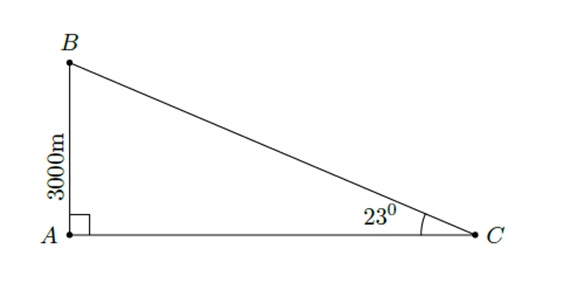
Muốn đạt độ cao $3 \, 000$ m so với mặt đất thì máy bay phải bay một đoạn đường là bao nhiêu mét? (kết quả làm tròn đến hàng đơn vị).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có hình vẽ minh họa.
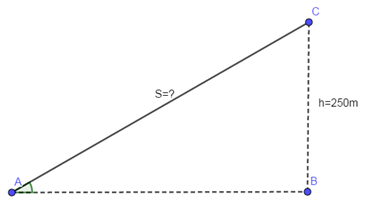
Độ dài đoạn AC chính là quãng đường máy bay cần đi để đạt độ cao 250m.
Xét tam giác ABC vuông tại B có:
sin(∠CAB)=BCAC⇒AC=BCsin(∠CAB)=hsin23o=250sin23o≈640(m)sin(∠CAB)=BCAC⇒AC=BCsin(∠CAB)=hsin23o=250sin23o≈640(m)
Vậy máy bay cần bay quãng đường 640 (m) để đạt được độ cao 250 (m).

Trong 2 phút, máy bay đi được: \(\frac{220.2}{60}=\frac{22}{3}\left(km\right)\)
Gọi mặt đất là AB, độ cao so với mặt đất sau 2 phút là AC, quãng đường máy bay đi được trong 2 phút là AC (theo hình vẽ)
Ta có: \(AC=BC.\sin ABC=\frac{22}{3}.\sin23^o\approx2,865\left(km\right)\)
Vậy máy bay ở độ cao 2,865 km so với mặt đất.

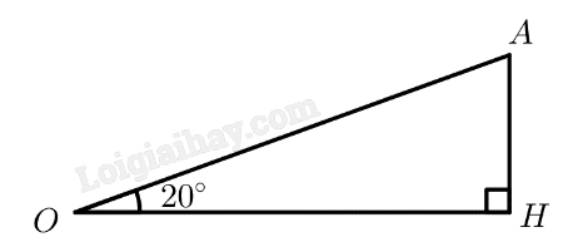
Đổi \(200km/h = \frac{{500}}{9}m/s\)
Mô hình hoá như hình vẽ, với \(OA\) là quãng đường máy bay bay được sau 2 giây, \(OH\) là độ cao của máy bay so với mặt đấy khi máy bay bay được sau 2 giây, độ lớn của góc \(\widehat {AOH}\) chỉ số đo góc giữa máy bay với mặt đất.
Sau 2 giây máy bay bay được quãng đường là: \(\frac{{500}}{9}.2 = \frac{{1000}}{9}\left( m \right)\)
Vì tam giác \(OAH\) vuông tại \(H\) nên ta có:
\(AH = OA.\sin \widehat {AOH} = \frac{{1000}}{9}.\sin {20^ \circ } \approx 38,0\left( m \right)\)
Vậy độ cao của máy bay so với mặt đất là 38 mét sau khi máy bay rời khỏi mặt đất 2 giây.

Hình vẽ bên minh họa một chiếc máy bay đang cất cánh từ sân bay. Đường bay lên tạo với phương nằm ngang một góc bằng 35 độ . Hỏi sau khi bay được quãng đường 10km thì máy bay ở độ cao bao nhiêu km so với mặt đất

a.
Nếu phi công muốn tạo góc nghiêng 5 độ so với mặt đất thì phải cách sân bay:
$\frac{8}{\sin 5^0}=91$ (km)
b.
Nếu cách sân bay 280 km máy bay bắt đầu hạ cạnh thì góc nghiêng là $\alpha$ thỏa mãn: $\frac{8}{\sin \alpha}=280$
$\sin \alpha= \frac{8}{280}=\frac{1}{35}$
$\Rightarrow \alpha = 1,64^0$

Độ cao của máy bay là cạnh góc vuông đối diện với góc 3 ° , khoảng cách từ máy bay đến sân bay là cạnh huyền
Vậy khoảng cách từ máy bay đến sân bay là:


Chọn C.
Phương pháp:
Gắn hệ trục tọa độ, xác định tọa độ điểm M trên parabol y = x 2 để độ dài đoạn AM nhỏ nhất.
Cách giải:
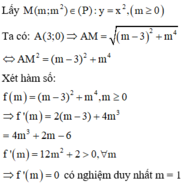
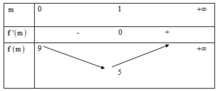
Ta có bảng biến thiên sau:
![]()
Muốn đạt độ cao 30003000 m so với mặt đất thì máy bay phải bay một đoạn đường dài:
\(BC=\dfrac{AB}{sin\left(23^o\right)}=\dfrac{3000}{sin\left(23^o\right)}\approx7678\left(m\right)\)
Kết luận: Muốn đạt độ cao 30003000 m so với mặt đất thì máy bay phải bay một đoạn đường dài gần 7678m