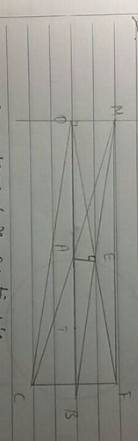
Cho góc vuông xOy và 2 điểm A, B trên tia Ox ( A ở giữa O và B) , M là 1 điểm bất kì trên tia Oy. Đường tròn t có đường kính AB cắt tia MA, MB lần lượt tại điểm thứ 2 là C, E. Tia OE cắt đường tròn tâm t tại điểm thứ 2 là F( E cùng phía với M, AM và AB)
a) CMR: O, A, E, M cùng thuộc 1 đường tròn, xác định tâm của đường tròn đó.
b) OCFM là hình gì, vì sao?
c) CMR: OE.OM + BE.BM =OB2
d) Xác định vị trí điểm M để tứ giác OCFM là hình bình hành , khi đó tìm mối liên hệ giữa OA và AB để OCFM là hình thoi.
MINA GIÚP MIK VS NHA< THANKS MỌI NGƯỜI NHÌU >.<

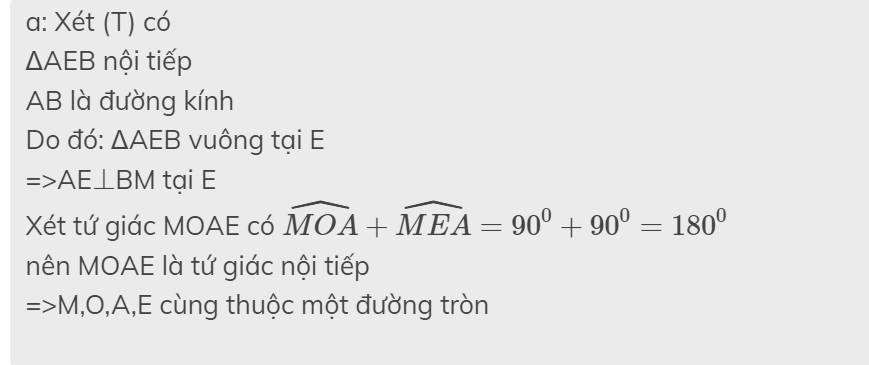



a) ta có góc AOM = 90 độ( gt góc xOy vuông)(1)
mặt khác ta có tam giác AEB nt đg tròn (t)
=> góc AEB=90 độ (2)
từ (1) (2) => tứ giác OAEM nội tiếp=> O,A,E,M
a) Ta thấy \(\widehat{AOM}=\widehat{AEM}=90^o\Rightarrow\) OAEM là tứ giác nội tiếp hay O, A, E, M cùng thuộc một đường tròn.
b) Do OAEM là tứ giác nội tiếp nên \(\widehat{AMO}=\widehat{AEO}\) (hai góc nội tiếp cùng chắn một cung)
Mà \(\widehat{AEO}=\widehat{ACF}\)(hai góc nội tiếp cùng chắn một cung)
Vì vậy nên \(\widehat{AMO}=\widehat{ACF}\) . Chúng lại ở vị trí so le trong nên CF // OM
Vậy OCFM là hình thang.
c) Câu này cô sửa lại đề. Theo cô phải là \(OE.OF+BE.BM=OB^2\) mới đúng.
Cô sẽ chứng minh theo đẳng thức đó.
Ta thấy ngay \(\Delta BEA\sim\Delta BOM\left(g-g\right)\Rightarrow\frac{BE}{BO}=\frac{BA}{BM}\Rightarrow BE.BM=OB.AB\)
Ta thấy rằng \(\widehat{BEF}+\widehat{BAF}=180^o=\widehat{OAF}+\widehat{BAF}\Rightarrow\widehat{BEF}=\widehat{OAF}\)
Vậy thì \(\Delta OAF\sim\Delta OEB\left(g-g\right)\Rightarrow\frac{OA}{OE}=\frac{OF}{OB}\Rightarrow OE.OF=OB.AO\)
Từ đó suy ra \(OE.OF+BE.BM=OB.AB+OB.AO=OB\left(BA+AO\right)=OB^2\)