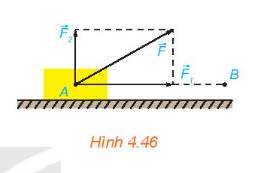
Phân tích được một lực thành hai lực thành phần vuông góc.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
nguyễn thị hương giang
15 tháng 11 2023
Đúng(2)
Những câu hỏi liên quan
VT
24 tháng 8 2017
Đáp án B.
Hai lực thành phần vuông góc nên F 2 = F 1 2 + F 2 2
VT
6 tháng 9 2017
Chọn đáp án B
F1 và F2 là hai lực vuông góc với nhau nên ta có:
VT
17 tháng 9 2018
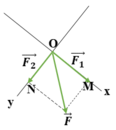
Phân tích lực là thay thế một lực bằng hai hay nhiều lực có tác dụng giống hệt như lực đó.
Cách phân tích lực:
+ Chọn hai phương Ox và Oy đi qua O là điểm đặt của lực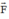 
cần phân tích. Hai phương này có biểu hiện tác dụng lực 
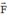gây ra.
+ Từ điểm mút của vecto F, kẻ các đoạn thẳng (bằng nét đứt) song song với Ox và Oy cắt hai phương này, ví dụ tại M và N ta được các vecto OM và ON biểu diển hai lực thành phần vecto F1 và vecto F2.
11 tháng 11 2021
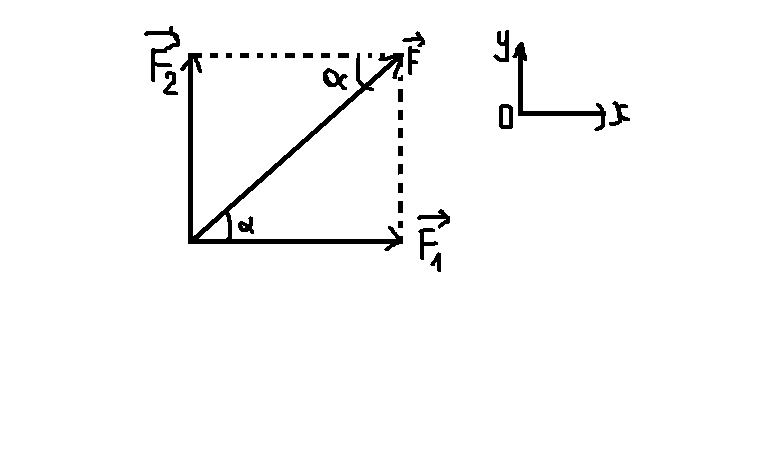
Chiếu lên trục tọa độ:
\(\Rightarrow F_1=Fcosa=10cos60=5N\)
\(F_2=Fsina=10\cdot sin60=5\sqrt{3}N\)
24 tháng 9 2023
Tham khảo:
a)
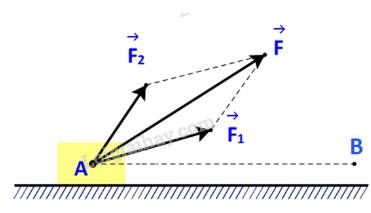
Gọi \(A,{A_1},{A_2}\) lần lượt là công sinh bởi lực \(\overrightarrow F \), \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \).
Ta cần chứng minh: \(A = {A_1} + {A_2}\)
Xét lực \(\overrightarrow F \), công sinh bởi lực \(\overrightarrow F \) là: \(A = \left| {\overrightarrow F } \right|.{\rm{ AB}}.\cos \left( {\overrightarrow F ,\overrightarrow {AB} } \right) = \overrightarrow F .\overrightarrow {AB} \)
Tương tự, ta có: \({A_1} = \overrightarrow {{F_1}} .\overrightarrow {AB} \), \({A_2} = \overrightarrow {{F_2}} .\overrightarrow {AB} \)
Áp dụng tính chất của tích vô hướng ta có:
\({A_1} + {A_2} = \overrightarrow {{F_1}} .\overrightarrow {AB} + \overrightarrow {{F_2}} .\overrightarrow {AB} = \left( {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right).\overrightarrow {AB} = \overrightarrow F .\overrightarrow {AB} = A\)
b)
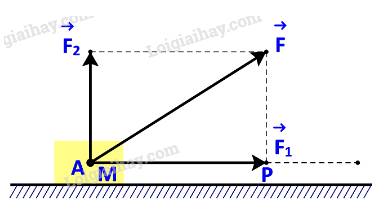
Vì \(\overrightarrow {{F_2}} \)tương ứng vuông góc với phương chuyển động nên \(\overrightarrow {{F_2}} \bot \overrightarrow {AB} \)
Do đó: công sinh bởi lực \(\overrightarrow {{F_2}} \) là: \({A_2} = \overrightarrow {{F_2}} .\overrightarrow {AB} = 0\)
Mà \(A = {A_1} + {A_2}\)
\( \Rightarrow A = {A_1}\)
Vậy công sinh bởi lực \(\overrightarrow F \) bằng công sinh bởi lực \(\overrightarrow {{F_1}} \).
VT
9 tháng 10 2018
Ta có:
F 1 → ⊥ F 2 → ⇒ F 2 = F 1 2 + F 2 2 ⇒ F 2 = F 2 − F 1 2 = 100 2 − 60 2 = 80 N
Đáp án: A