Cho dãy số u1=-2;un+1=un+n-1(n€N) Số hạng thứ 5 của dãy số là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
XC
1
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
\(u_n=u_1\cdot q^{n-1}\\ \Rightarrow\dfrac{3}{512}=\dfrac{3}{2}\cdot\left(\dfrac{1}{2}\right)^{n-1}\\ \Leftrightarrow\left(\dfrac{1}{2}\right)^{n-1}=\dfrac{1}{256}\\ \Leftrightarrow\left(\dfrac{1}{2}\right)^{n-1}=\dfrac{1}{2^8}\\ \Leftrightarrow n-1=8\\ \Leftrightarrow n=9\)
Vậy \(\dfrac{3}{512}\) là số hạng thứ 9 của dãy.
CM
1 tháng 11 2019
Chọn B.
Phương pháp:
Công thức tính tổng n số hạng đầu tiên của cấp số cộng có số hạng đầu u1 và công sai d
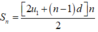
Cách giải:
Ta có: u n + 1 = u n + 2 , ∀ n ∈ ℕ *
⇒ ( u n ) là cấp số cộng có u 1 = - 5 , d = 2
M
30 tháng 8 2023
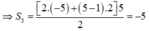
a) Để tính các số hạng u1, u2, u3, u4 của dãy (un), ta thay n = 1, 2, 3, 4 vào công thức un = n^2 - 1:
u1 = 1^2 - 1 = 0 u2 = 2^2 - 1 = 3 u3 = 3^2 - 1 = 8 u4 = 4^2 - 1 = 15
Vậy u1 = 0, u2 = 3, u3 = 8, u4 = 15.
b) Để tìm số hạng thứ mấy trong dãy có giá trị 99, ta giải phương trình n^2 - 1 = 99:
n^2 - 1 = 99 n^2 = 100 n = 10 hoặc n = -10
Vì số hạng của dãy phải là số tự nhiên nên ta chọn n = 10. Vậy số hạng thứ mấy có giá trị 99 là u10.
a) Để tính các số hạng u1, u2, u3, u4 của dãy (un), ta thay n = 1, 2, 3, 4 vào công thức un = (2n - 1)/(n + 1):u1 = (21 - 1)/(1 + 1) = 1/2 u2 = (22 - 1)/(2 + 1) = 3/3 = 1 u3 = (23 - 1)/(3 + 1) = 5/4 u4 = (24 - 1)/(4 + 1) = 7/5
Vậy u1 = 1/2, u2 = 1, u3 = 5/4, u4 = 7/5.
b) Để tìm số hạng thứ mấy trong dãy có giá trị 137137, ta giải phương trình (2n - 1)/(n + 1) = 137137:
(2n - 1)/(n + 1) = 137137 2n - 1 = 137137(n + 1) 2n - 1 = 137137n + 137137 137135n = 137138 n = 1
Vậy số hạng thứ mấy có giá trị 137137 là u1.
CM
23 tháng 3 2019
Chọn A.
Dễ thấy un là cấp số nhân với q = 10
Ta có: u8 = 107u1; u10 = 109u1
Do đó PT 
Giải PT ta được logu1 = -17 ⇔ u1 = 10-17 ⇒ u2018 = 102017 u1 = 102000
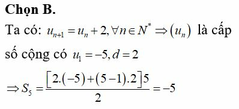
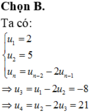
Ta có u2=u1+1=5?2=?1+1=5; u3=u2+2=7?3=?2+2=7; u4=u3+3=10?4=
?3+3=10. Do đó số hạng thứ 55 của dãy số là u5=u4+4=14?5=?4+4=14.
Vậy đáp án đúng 14