 làm chi tiết theo chương trình mới lớp 8 ạ
làm chi tiết theo chương trình mới lớp 8 ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
=>AEDF là hình chữ nhật
=>AD cắt EF tại trung điểm của mỗi đường
mà I là trung điểm của EF
nên I là trung điểm của AD
=>A,I,D thẳng hàng
b: Xét ΔBAC có DE//AC
nên \(\dfrac{DE}{AC}=\dfrac{BD}{BC}\)
Xét ΔBAC có DF//AB
nên \(\dfrac{DF}{AB}=\dfrac{CD}{CB}\)
\(\dfrac{DE}{AC}+\dfrac{DF}{AB}=\dfrac{BD}{BC}+\dfrac{CD}{BC}=1\)
=>\(\dfrac{DE}{AB}+\dfrac{DF}{AB}=1\)
=>\(DE+DF=AB\)
=>\(2\cdot\left(DE+DF\right)=2AB\)
=>\(C_{AEDF}=2\cdot AB\) không đổi

a: BC=căn 6^2+8^2=10cm
AB<AC<BC
=>góc C<góc B<góc A
b: Xét ΔCDB có
CA,DK là trung tuyến
CA cắt DK tại M
=>M là trọng tâm
=>CM=2/3CA=16/3(cm)
c: Q nằm trên trung trực của AC
=>QA=QC và góc QCA=góc QAC
=>góc QAD=góc QDA
=>QA=QD=QC
=>Q là trung điểm của CD
=>B,M,Q thẳng hàng

\(\dfrac{x+2}{x-3}< 0\)vì \(x+2>x-3\)
\(\left\{{}\begin{matrix}x+2>0\\x-3< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>-2\\x< 3\end{matrix}\right.\)<=> -2 < x < 3

5:
a: \(-120x^5y^4=20x^5y^2\cdot\left(-6y^2\right)\)
b: \(60x^6y^2=20x^5y^2\cdot3x\)
c: \(-5x^{15}y^3=20x^5y^2\cdot\left(-\dfrac{1}{4}x^{10}y\right)\)
d: \(2x^{12}y^{10}=20x^5y^2\cdot\left(\dfrac{1}{10}x^7y^8\right)\)

a)
Gọi hợp chất đó là A
dh/chất/H2 = 81 =) MA = 81 x 2 = 162 (g/mol)
CTHH : CxHyNz
Khối lượng của mỗi nguyên tố có trong 1 mol khí A là :
mC = \(\frac{162\times74,07\%}{100\%}=119,9934\approx120\)
mN = \(\frac{162\times17,28\%}{100\%}=27,9936\approx28\)
mH = \(\frac{162\times8,64\%}{100\%}=13,9968\approx14\)
Số mol nguyên tử của mỗi nguyên tố trong 1mol khí A là
\(n_H=\frac{m}{M}=\frac{14}{1}=14\left(mol\right)\)
\(n_C=\frac{m}{M}=\frac{120}{12}=10\left(mol\right)\)
\(n_N=\frac{m}{M}=\frac{28}{14}=2\left(mol\right)\)
=) Trong 1 mol phân tử hợp chất A có : 14 nguyên tử H , 10 nguyên tử C và 2 nguyên tử N
CTHH là : \(C_{10}H_{14}N_2\)
b) Bạn tự làm nha =)))
Chúc bạn học tốt ![]()


Ta có:
\(3x-3=3\left(x-1\right)\)
\(4-4x=-4\left(x-1\right)\)
\(x^2-1=\left(x-1\right)\left(x+1\right)\)
\(\Rightarrow\) MTC là \(3.\left(-4\right).\left(x-1\right)\left(x+1\right)=-12\left(x-1\right)\left(x+1\right)\)
Do đó:
\(\dfrac{11x}{3x-3}=\dfrac{11x}{3\left(x-1\right)}=\dfrac{11x.\left(-4\right).\left(x+1\right)}{3\left(x-1\right).\left(-4\right)\left(x+1\right)}=\dfrac{-44x\left(x+1\right)}{-12\left(x-1\right)\left(x+1\right)}\)
\(\dfrac{5}{4-4x}=\dfrac{5}{-4\left(x-1\right)}=\dfrac{5.3\left(x+1\right)}{-4\left(x-1\right).3\left(x+1\right)}=\dfrac{15\left(x+1\right)}{-12\left(x-1\right)\left(x+1\right)}\)
\(\dfrac{2x}{x^2-1}=\dfrac{2x}{\left(x-1\right)\left(x+1\right)}=\dfrac{2x.\left(-12\right)}{-12\left(x-1\right)\left(x+1\right)}=\dfrac{-24x}{-12\left(x-1\right)\left(x+1\right)}\)



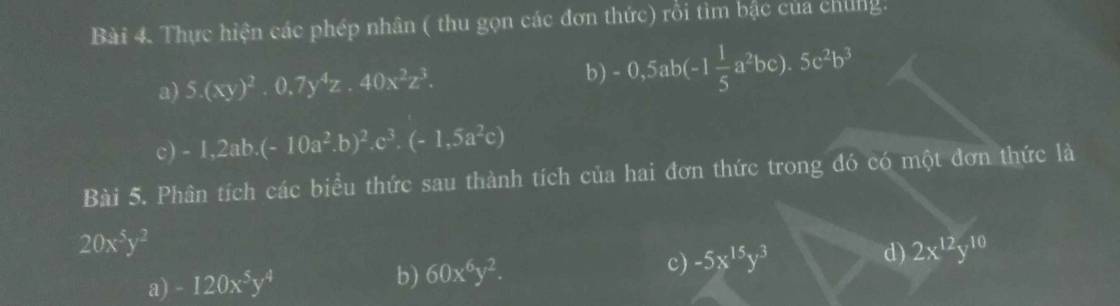


a: ΔABC vuông tại A
mà AM là đường trung tuyến
nên \(AM=MB=MC=\dfrac{BC}{2}\)
Xét ΔBAM có
MA=MB
Do đó: ΔBAM cân tại M
Xét ΔMAB cân tại M có \(\widehat{MBA}=60^0\)
nên ΔMAB đều
b: ΔMAB đều
mà BH là đường cao
nên H là trung điểm của AM
Xét ΔHMN vuông tại H và ΔHAB vuông tại H có
HA=HM
\(\widehat{HMN}=\widehat{HAB}\)
Do đó: ΔHMN=ΔHAB
=>HN=HB
Xét tứ giác ABMN có
H là trung điểm chung của AM và BN
nên ABMN là hình bình hành
=>AN//MB và AN=MB
AN=MB
MB=MC
Do đó: AN=MC
AN//MB
\(M\in BC\)
Do đó: AN//MC
Xét tứ giác AMCN có
AN//CM
AN=CM
Do đó: AMCN là hình bình hành
Hình bình hành AMCN có AC\(\perp\)MN
nên AMCN là hình thoi
c: ABMN là hình bình hành
=>\(\widehat{NMB}+\widehat{MBA}=180^0\)
=>\(\widehat{NMB}=120^0\)
Hình bình hành ABMN có NB\(\perp\)AM
nên ABMN là hình thoi
Xét ΔNMB có \(\dfrac{NB}{sinNMB}=\dfrac{BM}{sinMNB}\)
=>\(\dfrac{NB}{sin120}=\dfrac{BM}{sin30}\)
=>\(NB=BM\cdot\sqrt{3}\)
Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}\)
=>\(\dfrac{AC}{2\cdot BM}=sin60=\dfrac{\sqrt{3}}{2}\)
=>\(AC=BM\cdot\sqrt{3}\)
=>AC=NB