Một đoạn mạch gồm 2 điện trở R1=6 om ×R=3 om mắc song song với nhau vào hai điểm có hiệu điện thế 6V A) Tính điện trở tương đương của đoạn mạch
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
24 tháng 12 2019
Đáp án D
Điện trở mạch mắc song song
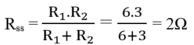
Cường độ dòng điện I = U/R = 6/2 = 3A
AM
23 tháng 12 2022
a. Điện trở tương đương của mạch:
\(R_{tđ}=\dfrac{R_1R_2}{R_1+R_2}=5\left(\Omega\right)\)
b. Cường độ dòng điện chạy qua điện trở R1 là:
\(I_1=\dfrac{U}{R_1}=2,4\left(A\right)\)
Cường độ dòng điện chạy qua điện trở R2 là:
\(I_2=\dfrac{U}{R_2}=2,4\left(A\right)\)
c. Điện trở tương đương của đoạn mạch lúc này là:
\(R_{tđ}'=R_{tđ}+R_đ=5+5=10\left(\Omega\right)\)
18 tháng 12 2021
\(\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3}=\dfrac{1}{10}+\dfrac{1}{10}+\dfrac{1}{10}=\dfrac{3}{10}\Omega\)
\(\Rightarrow R_{tđ}=\dfrac{10}{3}\Omega\)
\(U_1=U_2=U_3=U=12V\)
\(I=\dfrac{U}{R}=\dfrac{12}{\dfrac{10}{3}}=3,6A\)
\(I_1=I_2=I_3=\dfrac{U_1}{R_1}=\dfrac{12}{10}=1,2A\)
Nếu mắc nối tiếp:
\(R_{tđ}=R_1+R_2+R_3=10+10+10=30\Omega\)
H9
HT.Phong (9A5)
CTVHS
26 tháng 10 2023
a) Điện trở tương đương của mạch là:
\(\dfrac{1}{R_{td}}=\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{16}=\dfrac{5}{16}\)
\(\Rightarrow R_{td}=\dfrac{16}{5}=3,2\Omega\)
b) CĐDĐ của mạch chính là:
\(I=\dfrac{U}{R_{td}}=\dfrac{24}{3,2}=7,5A\)
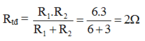
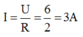
Điện trở tương đương của mạch là:
\(R_{tđ}=\dfrac{R_1R_2}{R_1+R_2}=\dfrac{6\cdot3}{6+3}=\dfrac{18}{9}=2\Omega\)