Tìm các phân số bằng nhau trong các phân số sau.
$\frac{2}{3}$ ; $\frac{3}{4}$ ; $\frac{9}{8}$ ; $\frac{9}{{12}}$ ; $\frac{6}{9}$
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\frac{1}{5}=\frac{1.3}{5.3}=\frac{3}{15}\)
\(\frac{-10}{55}=\frac{-10\div5}{55\div5}=\frac{-2}{11}\)
Vậy ba cặp số phân số bằng nhau sau khi sử dụng tính chất cơ bản
2 .
\(\frac{-12}{-3}=\frac{-12:3}{-3:3}=\frac{-4}{-1};\frac{7}{-35}=\frac{7:7}{-35:7}=\frac{1}{-5};\frac{-9}{27}=\frac{-9:9}{27:9}=\frac{-1}{3}\)
3 .
\(15min=\frac{1}{4}\)giờ
\(90min=\frac{3}{2}\)giờ

Tham khảo:
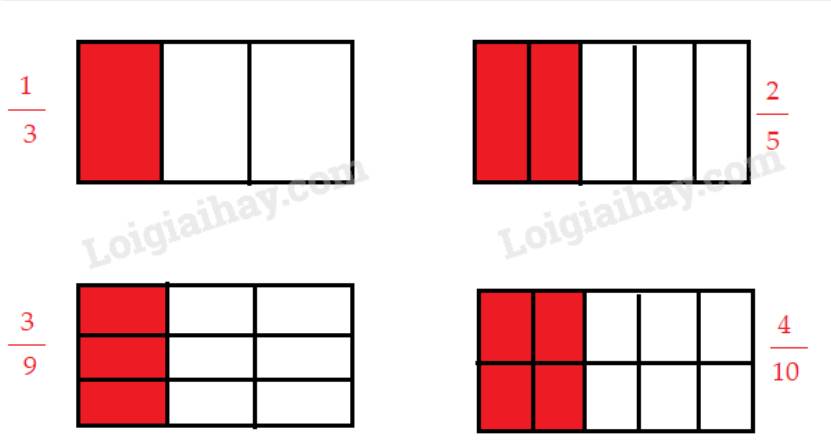
Như vậy,\(\dfrac{2}{5} = \dfrac{4}{{10}}\)
\(\dfrac{1}{3} = \dfrac{3}{9}\)

Các phân số bằng nhau là: 3 − 5 = − 27 45 ; 11 66 = 3 18 ; 13 26 = 17 34 ; − 5 − 7 = 25 35 .

Các cặp phân số đối nhau là:
\(\frac{{ - 5}}{6}\) và \(\frac{5}{6}\) (vì \(\frac{{ - 5}}{6}+\frac{5}{6}=0\))
\(\frac{{ - 40}}{{ - 10}}\) và \(\frac{{40}}{{ - 10}}\) (vì \(\frac{{ - 40}}{{ - 10}}+\frac{{40}}{{ - 10}}=4+(-4)=0\))
\(\frac{5}{6}\) và \(\frac{{10}}{{ - 12}}\) (vì \(\frac{5}{6} +\frac{{10}}{{ - 12}}=0\))
\(-\dfrac{5}{6};\dfrac{5}{6}\)
\(\dfrac{-40}{-10};\dfrac{40}{-10}\)
\(\dfrac{10}{-12};\dfrac{5}{6}\)

Rút gọn các phân số chưa tối giản để xuất hiện các phân số bằng nhau.
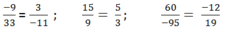

Phân số bằng nhau là
* \(\frac{25}{35}=\frac{5}{7}\) Và \(\frac{55}{77}=\frac{5}{7}\)
\(\Rightarrow\frac{25}{35}=\frac{55}{77}\)
Các câu khác tương tự bạn nhé(Nhớ tích cho mk nha)

Ta rút gọn các phân số về dạng tối giản:
Do vậy ta có:
Phân số 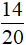
Ta rút gọn các phân số về dạng tối giản:
Do vậy ta có:
Phân số 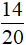
$\frac{2}{3} = \frac{{2 \times 3}}{{3 \times 3}} = \frac{6}{9}$
$\frac{3}{4} = \frac{{3 \times 3}}{{4 \times 3}} = \frac{9}{{12}}$
Vậy $\frac{2}{3} = \frac{6}{9}$ ; $\frac{3}{4} = \frac{9}{{12}}$
\(\dfrac{2}{3}=\dfrac{6}{9}\)
\(\dfrac{3}{4}=\dfrac{9}{12}\)