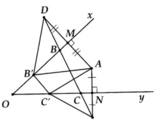
Cho góc nhọn xOy và hai điểm A và B thuộc miền trong của góc. Tìm các điểm C, D lần lượt thuộc Ox và Oy sao cho đường gấp khúc ACDBA bé nhất.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án A

Lấy A’, A” lần lượt là điểm đối xứng với A qua Ox và Oy
Tacó:
AB + AC + BC = BA’ + CA” + BC ≥ A’A” Chu vi tam giác ABC:
Dấu bằng xảy ra khi A’, A” , B , C thẳng hàng

a: ΔOAB cân tại O
mà OI là phân giác
nên OI vuông góc AB và OI là trung trực của AB
b: Xét ΔOAB có
OI,AD là đường cao
OI cắt AD tại C
=>C là trực tâm
=>BC vuông góc Ox tại E
c: Xét ΔODA vuông tại D và ΔOEB vuông tại E có
OA=OB
góc DOA chung
=>ΔODA=ΔOEB
=>OD=OE
Xét ΔOAB có OE/OA=OD/OB
nên ED//AB

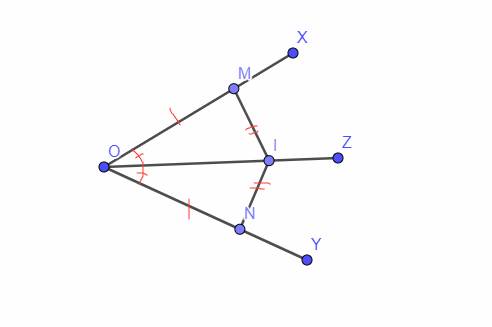
`a,` Xét Tam giác `OIM` và Tam giác `OIN` có:
`OM = ON (g``t)`
\(\widehat{MOI}=\widehat{NOI}\) `(` tia phân giác \(\widehat{xOy}\) `)`
`OI` chung
`=>` Tam giác `OIM =` Tam giác `OIN (c-g-c)`
`b,` Vì Tam giác `OIM =` Tam giác `OIN (a)`
`->` \(\widehat{OIM}=\widehat{OIN}\) `( 2` góc tương ứng `)`
`c,` Vì Tam giác `OIM =` Tam giác `OIN (a)`
`-> IM = IN (2` cạnh tương ứng `)`
`\color{blue}\text {#DuyNam}`

a: Xét ΔOAE vuông tại A và ΔOBF vuông tại B có
OA=OB
góc O chung
Do đó: ΔOAE=ΔOBF
=>OE=OF
b: Xét ΔABE và ΔBAF có
AB chung
BE=AF
AE=BF
Do đó: ΔABE=ΔBAF
=>góc BAE=góc ABF
c: Xét ΔIAB có góc IAB=góc IBA
nên ΔIAB cân tại I
=>IA=IB
mà OA=OB
nên OI là trung trực của AB
=>OI vuông góc với AB