Thực hành: Tung một đồng xu 20 lần liên tiếp. Sử dụng vạch kiểm để kiểm đếm và hoàn thành bảng sau.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 6 2023
a: Số lần xuất hiện mặt S: 9
Số lần xuất hiện mặt N: 11
b: P(S)=9/20
P(N)=11/20
14 tháng 1
Xác suất thực nghiệm của biến cố ngẫu nhiên "Mặt xuất hiện của đồng xu là mặt N" là \(\dfrac{8}{15}\)
Xác suất thực nghiệm này bằng với xác suất của biến cố ngẫu nhiên ở trên
HQ
Hà Quang Minh
Giáo viên
8 tháng 10 2023
Số lần ghim chỉ vào ô màu trắng là 12
Tỉ số của số lần ghim chỉ vào ô màu trắng và tổng số lần xoay là: 12: 20 = \(\frac{3}{5}\)
8 tháng 10 2023
Số lần chỉ ghim vào ô màu trắng là 12
Tỉ số giữa số lần chỉ ghim vào ô trắng và tổng số lần là:\(\dfrac{12}{20}=\dfrac{3}{5}\)
27 tháng 11 2023
Tham khảo:
a)
b)
c)
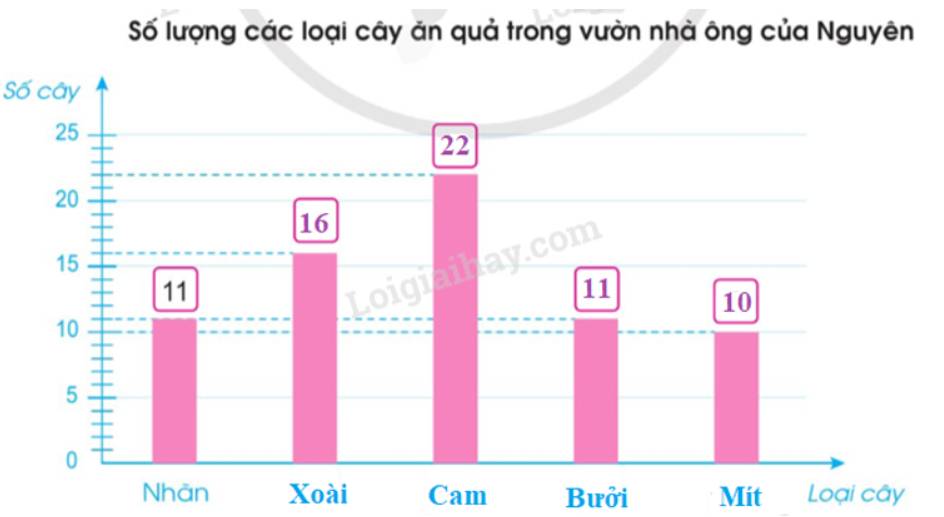
- Nguyên đã kiểm đếm những loại cây trong vườn nhà ông là: Nhãn, xoài, cam, bưởi, mít.
- Trong các loại cây Nguyên kiểm đếm, loại cây có số lượng nhiều nhất là cam, loại cây có số lượng ít nhất là mít, loài cây có số lượng bằng nhau là nhãn và bưởi.
- Nguyên đã kiểm đếm tất cả số cây là: 11 + 16 + 22 + 11 + 10 = 70 (cây)
- Trung bình mỗi loại cây ăn quả trong vườn nhà ông có số cây là: 70 : 5 = 14 (cây)
16 tháng 2 2022
a, Xác suất thực nghiệm xuất hiện mặt N là:\(\frac{13}{22}\)
b,Xác suất thực nghiệm xuất hiện mặt S là:\(\frac{11}{25}\)
c,Số lần xuất hiện mặt S là: 30 - 14 = 16
,Xác suất thực nghiệm xuất hiện mặt S là:\(\frac{16}{30}\)
NV
Nguyễn Việt Dũng
CTVVIP
31 tháng 10 2023
Sau 5 lần tung đồng xu:
- Số lần xuất hiện mặt N là 3 lần
- Số lần xuất hiện mặt S là 2 lần
MN
18 tháng 4 2021
a) Nếu tung một đồng xu 22 lần liên tiếp; có 13 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt N bằng: \(\dfrac{13}{22}\)
b) Nếu tung một đồng xu 25 lần liên tiếp; có 11 lần xuất hiện mặt S thì xác suất thực nghiệm xuất hiện mặt S bằng: \(\dfrac{11}{25}\)
c) Nếu tung một đồng xu 30 lần liên tiếp; có 14 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt S bằng: \(\dfrac{30-14}{30}=\dfrac{8}{15}\)
19 tháng 1 2022
Xác suất thực nghiệm xuất hiện mặt N là: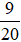 
Vậy xác suất thực nghiệm xuất hiện mặt N là: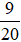
Học sinh tự thực hành và điền kết quả vào bảng.