Giúp với 🥲🥲
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)\(-1,6:\left(1+\dfrac{2}{3}\right)=-1,6:\dfrac{5}{3}=-\dfrac{8}{5}.\dfrac{3}{5}=\dfrac{-24}{25}\)
b)\(\left(\dfrac{-2}{3}\right)+\dfrac{3}{4}-\left(-\dfrac{1}{6}\right)+\left(\dfrac{-2}{5}\right)=-\dfrac{2}{3}+\dfrac{3}{4}+\dfrac{1}{6}-\dfrac{2}{5}=\dfrac{-40+45+10-24}{60}=\dfrac{-9}{60}=\dfrac{-3}{20}\)
c)\(\left(\dfrac{-3}{7}:\dfrac{2}{11}+\dfrac{-4}{7}:\dfrac{2}{11}\right).\dfrac{7}{33}=\left(\dfrac{-3}{7}.\dfrac{11}{2}+\dfrac{-4}{7}.\dfrac{11}{2}\right).\dfrac{7}{33}=\left[\dfrac{11}{2}\left(\dfrac{-3}{7}+\dfrac{-4}{7}\right)\right].\dfrac{7}{33}=\dfrac{-11}{2}.\dfrac{7}{33}=\dfrac{-7}{6}\)
d)\(\dfrac{-5}{8}+\dfrac{4}{9}:\left(\dfrac{-2}{3}\right)-\dfrac{7}{20}.\left(\dfrac{-5}{14}\right)=\dfrac{-5}{8}-\dfrac{4}{9}.\dfrac{3}{2}+\dfrac{1}{8}=\dfrac{-5}{8}+\dfrac{1}{8}-\dfrac{2}{3}=-\dfrac{7}{6}\)



1 correct
2 success => only success
3 was released => released
4 correct
5 focused on => on
6 as a => a
7 correct
8 each others => others
9 satisfy with => satisfy
10 correct
11 correct

1 were - would you play
2 weren't studying - would have
3 had taken - wouldn't have got
4 would you go - could
5 will you give - is
6 recycle - won't be
7 had heard - wouldn't have gone
8 would you buy - had
9 don't hurry - will miss
10 had phoned - would have given
11 were - wouldn't eat
12 will go - rains
13 had known - would have sent
14 won't feel - swims
15 hadn't freezed - would have gone

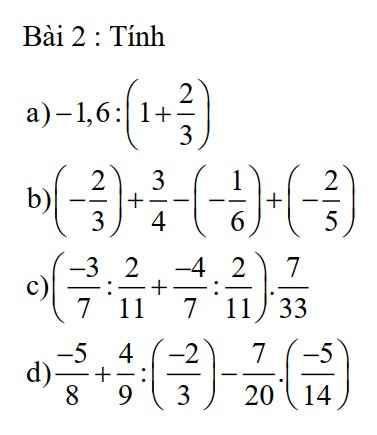 giúp với giúp với giúp e với ạ. e cảm ơn
giúp với giúp với giúp e với ạ. e cảm ơn

 Ai giúp mình với ạ
Ai giúp mình với ạ


a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=9+144=153\)
=>\(BC=3\sqrt{17}\left(cm\right)\)
Xét ΔABC vuông tại A có
\(tanB=\dfrac{AC}{AB}=4\)
=>\(\widehat{B}\simeq75^057'\)
c: Xét tứ giác AMHN có \(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)
nên AMHN là hình chữ nhật
Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
=>\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Xét ΔAMN vuông tại A và ΔACB vuông tại A có
\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Do đó: ΔAMN\(\sim\)ΔACB