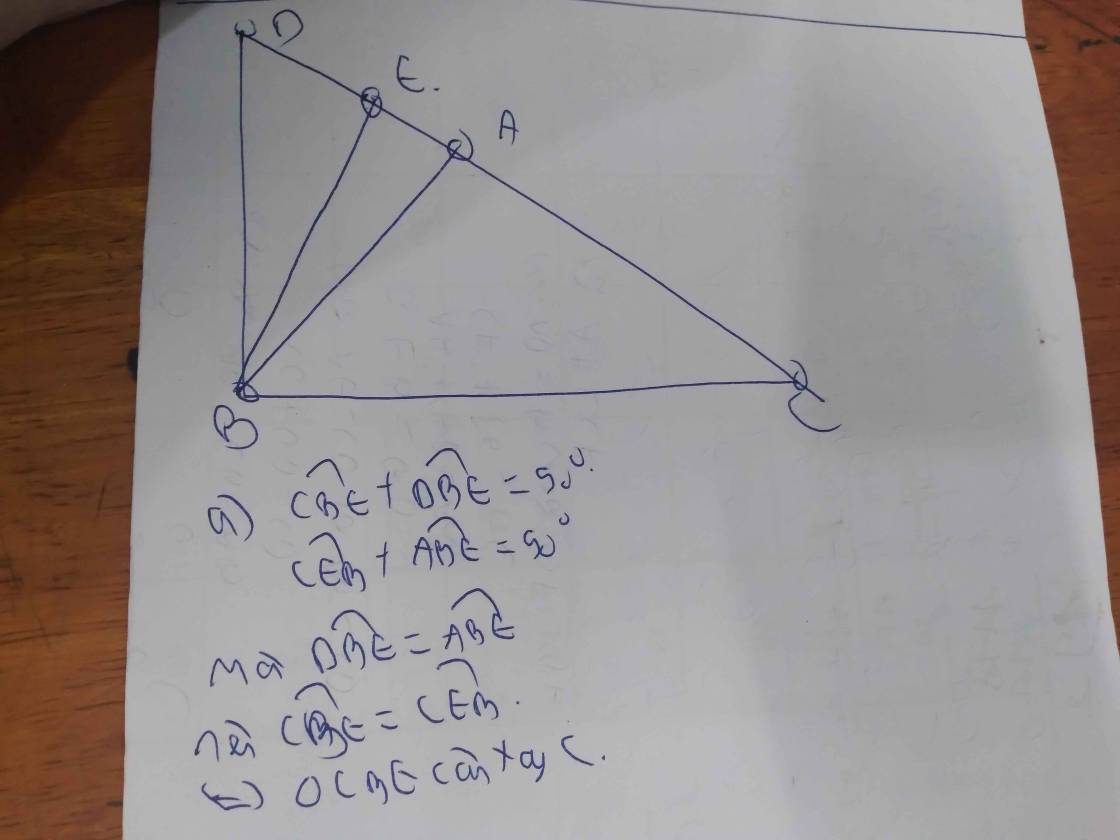
Cho △ABC vuông tại A có đường cao AH. Đường thẳng đi qua điểm B và vuống góc với BC cắt AC tại D a) Tia phân giác của góc ABD cắt AD tại E. Chứng minh △BCE cânb) Chứng minh: AB.EC ANCD

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

T

Tuyết

28 tháng 10 2023

Cho △ABC vuông tại A có đường cao AH. Đường thẳng đi qua điểm B và vuống góc với BC cắt AC tại D a) Tia phân giác của góc ABD cắt AD tại E. Chứng minh △BCE cânb) Chứng minh: AB.EC+ANCD ...

1

NL

Nguyễn Lê Phước Thịnh

28 tháng 10 2023

loading...

Những câu hỏi liên quan

KB

Không Biết

16 tháng 3 2016 - olm

cho tam giác ABC vuông tại A. Đường cao AH, phân giác của góc A cắt cạnh huyền BC tại D. Qua D kẻ đường thẳng vuông góc với BC cắt AC ở E và AB ở F chứng minh AB.EC=BC.DE

1

DL

Đỗ Lương Hoàng Anh

16 tháng 3 2016

(mình k pk kẻ hình bn nhé)

ta có Scbe=1/2*AB*EC=1/2*ED*BC

suy ra AB.EC=BC.DE

TD

Tiến Đạt

13 tháng 2 2020 - olm

Cho tam giác ABC vuông tại A, đường cao AH. Tia phân giác của góc CAH cắt cạnh BC tại E .Đường thẳng qua E vuông góc với BC cắt AC tại D. Gọi I là giao điểm của AH và BD.

a) Chứng minh tam giác BAE cân tại B và BD là đường trung trực của AE

b) Chứng minh EI // AC

c) So sánh AD và DC

d) Chứng minh AH + BC > AB + AC

0

B

Biokgnbnb

6 tháng 12 2015 - olm

Cho tam giác ABC vuông tại A, đường cao AH, tia phân giác góc HAC cắt BC tại D.

a. CMR tam giác ABD cân

b. Từ B kẻ đường thẳng vuông góc với AD cắt AC tại M. Chứng minh rằng MD//AH

c. Gọi E là giao điểm của AH và MB. CMR MD=AE

1

ND

NGUYỄN ĐỨC DIỆN

19 tháng 3 2021

dễ quá k làm nx

XM

Xuân Mẫn Ngô Ngọc

27 tháng 2 2022

Cho tam giác aBC vuông tại A , Có góc C =30' . tia phân giác của góc B cắt tại AC tại D . Vẽ DE vuông góc với BC tại E . Qua điểm C vẽ đường thẳng vuông góc với tia BD tại H .

a. Chứng minh : tam giác ABD= tam giác EBD

b. Tính góc DBC và chứng minh : DB=DC

c. So Sánh : HC và HD

1

NL

Nguyễn Lê Phước Thịnh

27 tháng 2 2022

a: XétΔABD vuông tại A và ΔEBD vuông tại E có

BD chung

\(\widehat{ABD}=\widehat{EBD}\)

Do đó: ΔABD=ΔEBD

b: \(\widehat{DBC}=\dfrac{60^0}{2}=30^0\)

Xét ΔDBC có \(\widehat{DBC}=\widehat{DCB}\)

nên ΔDBC cân tại D

HA

Hoàng Anh Thư

26 tháng 3 2022

Cho ∆ABC vuông tại A. Tia phân giác của góc ABC cắt AC tại D. Vẽ DE ⊥ BC tại E. a) Chứng minh ∆ABD = ∆EBD b) Chứng minh : AD = ED c) Qua điểm C vẽ đường vuông góc với CA cắt BD tại K. So sánh CK và AC giúp mik đi mà mik đang cần...

1

LM

Luna Milk

26 tháng 3 2022

a) Xét 2 tam giac vuông tam giác ABD và tam giác EBD
ta có BD là cạnh chung
ABD=EBD(gt)
Do đó tam giác ABD= tam giác EBD(cạnh huyền góc nhọn)

BN

Bao Ngoc

8 tháng 6 2016 - olm

Bài 1: Tam giác ABC cân tại A ( góc A > 90 độ). Hai đường cao BD và CE cắt nhau tại H. Tia AH cắt BC tai Ia) Chứng minh tam giác ABD = tam giác ACEb) Chứng minh I là trung điểm của BCc) Từ C kẻ đường thẳng d vuông góc với AC. d cắt đường thẳng AH tại F. Chứng minh CB là tia phân giác của góc FCHd) Giả sử góc BAC = 60 độ, AB = 4cm. Tính khoảng cách từ B đến đường thẳng CFBài 2: Tam giác ABC vuông tại A...

1

OB

Oo Bản tình ca ác quỷ oO

8 tháng 6 2016

nhìu zữ giải hết chắc chết!!!

758768768978980

D

Dyuvils

7 tháng 12 2023

Cho ΔABC vuông tại A, đường cao AH. Tia phân giác của góc B cắt AC tại D. Từ D kẻ DE vuông góc với BC ( E thuộc BC ). Chứng minh AB.EC=EH.BC

1

NL

Nguyễn Lê Phước Thịnh

7 tháng 12 2023

Ta có: DE\(\perp\)BC

AH\(\perp\)BC

Do đó: DE//AH

Xét ΔCAH có DE//AH

nên \(\dfrac{CE}{EH}=\dfrac{CD}{DA}\)(1)

Xét ΔABC có BD là phân giác

nên \(\dfrac{CD}{DA}=\dfrac{CB}{BA}\left(2\right)\)

Từ (1) và (2) suy ra \(\dfrac{CE}{EH}=\dfrac{CB}{BA}\)

=>\(CE\cdot BA=EH\cdot BC\)

H

hoangtuvi

8 tháng 5 2021

Cho ABC vuông tại A,AB<AC , đường cao AH . Trên cạnhAC , lấy điểm E sao cho AH=AE . Qua E kẻ đường thẳng vuông góc vớiAC , cắt cạnh BC tại D .a) Chứng minh tam giác AHD = tam giác AHE và AD là tia phân giác của tam giác HACb) Tia ED cắt tia AH tại K . Chứng minh KCD cân.c) So sánh HK và AKd) Gọi I là trung điểm của KC , chứng minh ba điểm A,D,I thẳng...

0

NT

Nguyệt Thanh Vân

2 tháng 12 2021

Cho tam giác ABC vuông tại A (AB< AC) AH là đường cao, Tia phân giác của góc CAH cắt BC tại D Qua D kẻ DK vuông góc AC tại K . Tia phân giác của góc ABC cắt DK tại E.a)Chứng minh tam giác BAD cânb)Chứng minh tứ giác ABDE là hình thoi.c)Tìm điều kiện của tam giác vuông ABC để tứ giác ABCE là hình thang...

0