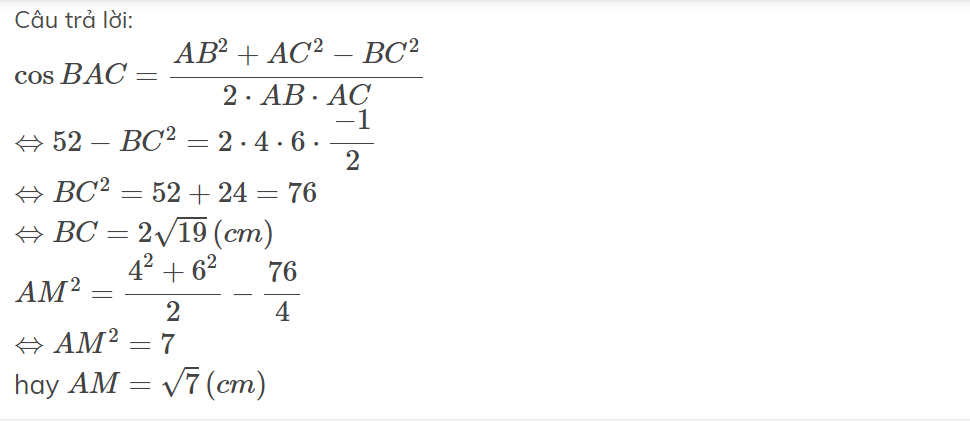Cho tam giác ABC có AB = 4 AC = 6 A = 120 độ Tính BC,S,ha,R.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.






Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot BA\cdot BC\cdot sinABC\)
\(=\dfrac{1}{2}\cdot5\cdot7\cdot sin120=\dfrac{35\sqrt{3}}{4}\)
Xét ΔABC có \(cosB=\dfrac{BA^2+BC^2-AC^2}{2\cdot BA\cdot BC}\)
=>\(\dfrac{5^2+7^2-AC^2}{2\cdot5\cdot7}=cos120=\dfrac{-1}{2}\)
=>\(25+49-AC^2=-35\)
=>\(AC^2=25+49+35=109\)
=>\(AC=\sqrt{109}\)
Kẻ AH\(\perp\)BC
=>\(h_A=AH\)
\(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC\)
=>\(\dfrac{1}{2}\cdot AH\cdot7=\dfrac{35\sqrt{3}}{4}\)
=>\(AH\cdot3,5=\dfrac{35\sqrt{3}}{4}\)
=>\(AH=\dfrac{10\sqrt{3}}{4}=\dfrac{5}{2}\sqrt{3}\)
Xét ΔABC có \(\dfrac{AC}{sinB}=2R\)
=>\(2R=\dfrac{\sqrt{109}}{sin120}=\sqrt{109}\cdot\dfrac{2}{\sqrt{3}}\)
=>\(R=\sqrt{\dfrac{109}{3}}=\dfrac{\sqrt{327}}{3}\)

3:
Đặt HB=x; HC=y
Theo đề, ta có: x+y=289 và xy=120^2=14400
=>x,y là các nghiệm của phương trình:
a^2-289a+14400=0
=>a=225 hoặc a=64
=>(x,y)=(225;64) và (x,y)=(64;225)
TH1: BH=225cm; CH=64cm
=>\(AB=\sqrt{225\cdot289}=15\cdot17=255\left(cm\right)\) và \(AC=\sqrt{64\cdot289}=7\cdot17=119\left(cm\right)\)
TH2: BH=64cm; CH=225cm
=>AB=119m; AC=255cm

Áp dụng định lí cô sin trong tam giác ta có:
B C 2 = A B 2 + A C 2 − 2 A B . A C . cos A = 4 2 + 6 2 − 2.4.6. cos 120 °
= 4 2 + 6 2 − 2.4.6. − 1 2 = 76 ⇒ B C = 76 = 2 19 .
Chọn B.


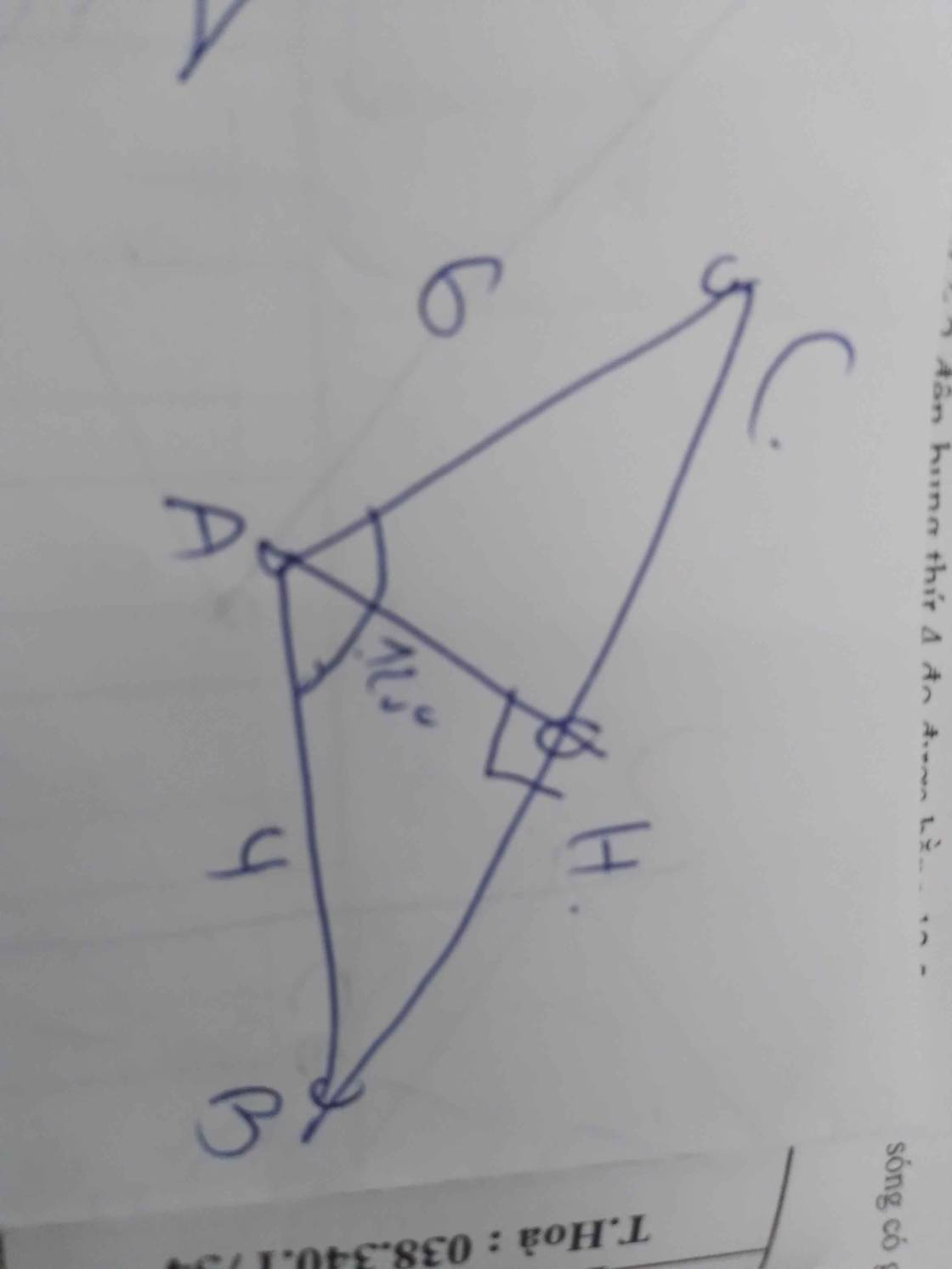
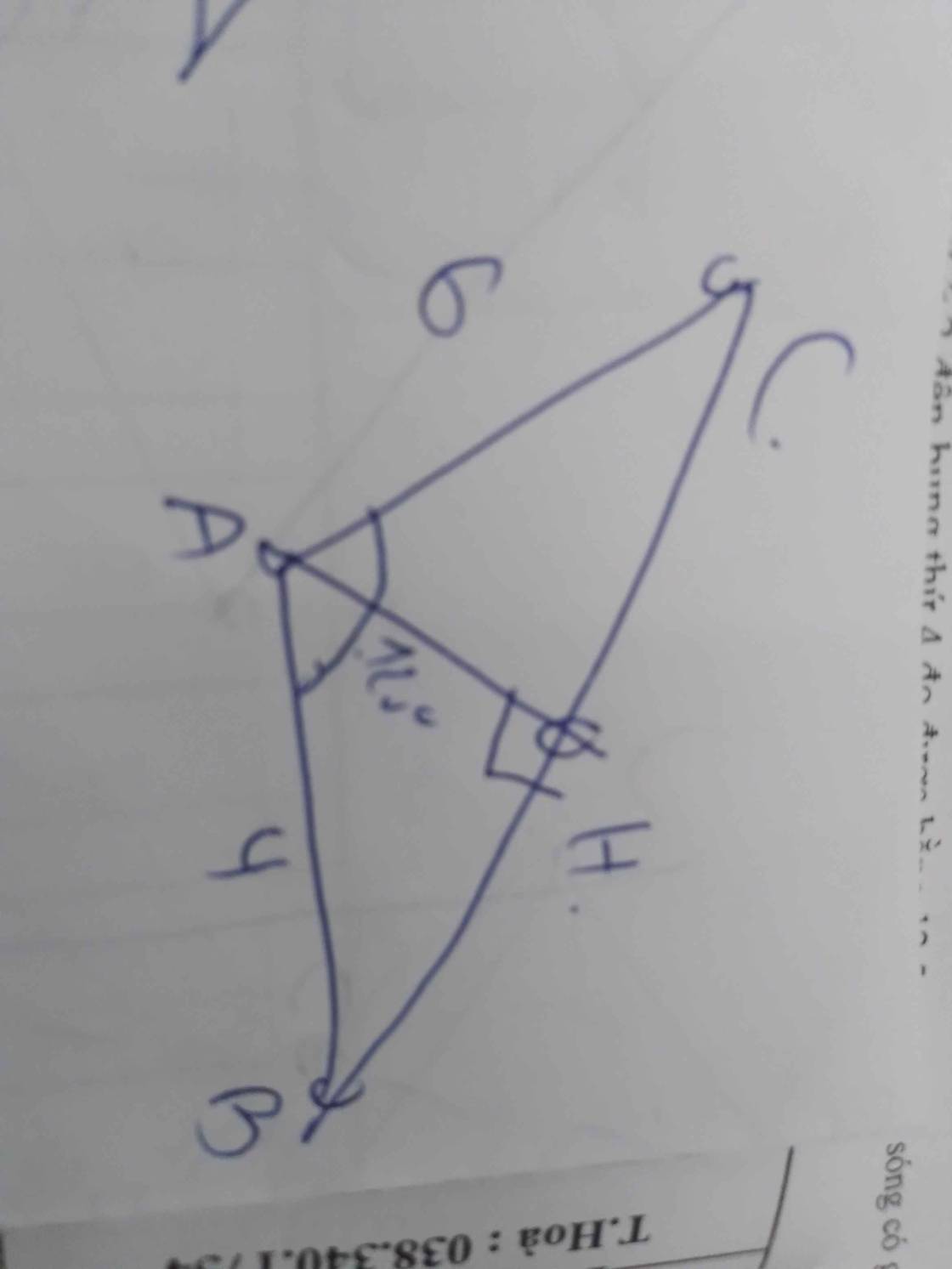
Hạ MH và BK vuông AC,
Ta thấy MH là đường tr.bình t.g BCK.
Có góc BÂK =60 độ
nên KA =AB/2 =2
và BK =2.căn3
=> MH =BK/2 = căn3.
Mặt khác KC =KA +AC =8
=> KH =KC/2 =4
=> AH =2. T
a lại có AM2 =AH^2+HM^2 =4+3 =7
nên AM = √7

Áp dụng định lí Cos : \(BC=\sqrt{AB^2+AC^2-2AB.AC.cos\widehat{BAC}}=\sqrt{4^2+6^2-2.4.6.cos120^o}=2\sqrt{19}\) (cm)
\(AM=\sqrt{\frac{AB^2+AC^2}{2}-\frac{BC^2}{4}}=...\)
2,65 ( làm tròn đến số thập phân số 2)
kết quả đúng mkf thử rồi![]()