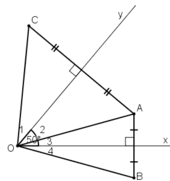
1. Cho góc xOy < 90 độ điểm A nằm trong góc đó.Gọi B là điển đối xứng với A qua Ox,C đối xứng với A qua Oy
a, CM : tam giác BOC cân
b, Cho góc xOy = 70 độ . Tính BÔC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 8 2021
a) Vì A và B đối xứng nhau qua Ox nên Ox là trung trực AB
⇒ OB = OA (tính chất cách đều)
Vì A và C đối xứng nhau qua Oy nên Oy là trung trực AC
⇒ OA = OC
⇒ OB = OC
⇒ ΔBOC cân tại O
b) Trong tam giác cân BOA có Ox đường cao
⇒ Ox phân giác của ∠BOA
⇒ ∠BOA = 2∠AOx
ΔAOC cân tại O có Oy đường cao
⇒ Oy phân giác góc BOC
⇒ ∠AOC = 2∠AOy
Và ∠BOC = ∠BOA + ∠AOC = 2
∠AOx + 2∠AOy = 2(∠AOx + ∠AOy) = 2∠xOy
⇒ ∠BOC = 2. 70o = 140o
25 tháng 10 2018
Gọi AB giao Ox tại M, AC giao Oy tại N
B đối xứng A qua Ox => OA = OB => tam giác ABO cân tại O => OM vừa là đường cao vừa là đường phân giác
=> góc AOM = góc MOB
C đối xứng A qua Oy => OA = OC => tam giác ACO cân tại O => ON vừa là đường cao vừa là đường phân giác
=> góc CON = góc NOA
BOC = CON + AON + AOM + BOM = 2xOy = 120o
17 tháng 10 2021
a: Ta có: A và B đối xứng nhau qua Ox
nên Ox là đường trung trực của AB
Suy ra: OA=OB(1)
Ta có: A và C đối xứng nhau qua Oy
nên Oy là đường trung trực của AC
Suy ra: OA=OC(2)
từ (1) và (2) suy ra OB=OC
hay ΔOBC cân tại O
CM
5 tháng 1 2020
a) + B đối xứng với A qua Ox
⇒ Ox là đường trung trực của AB
⇒ OA = OB (1)
+ C đối xứng với A qua Oy
⇒ Oy là đường trung trực của AC
⇒ OA = OC (2)
Từ (1) và (2) suy ra OB = OC (= OA)
b) + ΔOAC cân tại O có Oy là đường trung trực
⇒ Oy đồng thời là đường phân giác
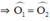
+ ΔOAB cân tại O có Ox là đường trung trực
⇒ Ox đồng thời là đường phân giác
7 tháng 11 2021
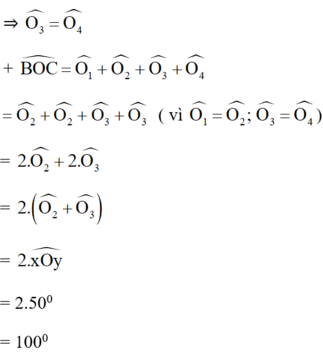
a: Ta có: A và B đối xứng nhau qua Ox
nên OA=OB(1)
Ta có: A và C đối xứng nhau qua Oy
nên OA=OC(2)
Từ (1) và (2) suy ra OB=OC
dễ mà tự suy nghĩ đi
Câu a là Xét Tam giác đúngko