Tìm các số thực x,y thoả mãn
2x2 + y2 - 2xy - 8x + 16 = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(5x^2+2xy+y^2-16x+16=0\)
=>\(x^2+2xy+y^2+4x^2-16x+16=0\)
=>\(\left(x+y\right)^2+\left(2x-4\right)^2=0\)
=>\(\left\{{}\begin{matrix}x+y=0\\2x-4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-2\end{matrix}\right.\)


\(\Leftrightarrow\left(x^2+2xy+y^2\right)+4\left(x+y\right)+4+\left(x^2-12x+36\right)=0\)
\(\Leftrightarrow\left(x+y\right)^2+4\left(x+y\right)+4+\left(x-6\right)^2=0\)
\(\Leftrightarrow\left(x+y+2\right)^2+\left(x-6\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-6=0\\x+y+2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=6\\y=-8\end{matrix}\right.\)
\(y^2+2xy-12x+4\left(x+y\right)+2x^2+40=0\\ \Leftrightarrow\left[\left(x^2+2xy+y^2\right)+4\left(x+y\right)+4\right]+\left(x^2-12x+36\right)=0\\ \Leftrightarrow\left(x+y+2\right)^2+\left(x-6\right)^2=0\)
Vì \(\left\{{}\begin{matrix}\left(x+y+2\right)^2\ge0\forall x,y\\\left(x-6\right)^2\ge0\forall x\end{matrix}\right.\)
Nên \(\left(x+y+2\right)^2+\left(x-6\right)^2\ge0\forall x,y\)
Dấu"=" xảy ra khi và chỉ khi:
\(\left\{{}\begin{matrix}x+y+2=0\\x-6=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-8\\x=6\end{matrix}\right.\)
Vậy x = 6 và y = -8


Áp dụng BĐT cói cho 2 số ko âm ta có
X^2+y^2 >= 2 .căn x^2 .y^2 = 2.xy= 2.6 =12
Vậy P min =12 dấu = xảy ra khi x^2=y^2 <=> x=y
( thông cảm mình gõ mũ ko đc )

\(P-\dfrac{5}{2}=x+2y-\dfrac{x^2+y^2}{2}=-\dfrac{1}{2}\left(x-1\right)^2-\dfrac{1}{2}\left(y-2\right)^2+\dfrac{5}{2}\le\dfrac{5}{2}\)
\(\Rightarrow P-\dfrac{5}{2}\le\dfrac{5}{2}\Rightarrow P\le5\)
\(P_{max}=5\) khi \(\left(x;y\right)=\left(1;2\right)\)
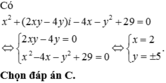

\(2x^2+y^2-2xy-8x+16=0\)
\(\Leftrightarrow\left(x^2-8x+16\right)+\left(x^2-2xy+y^2\right)=0\)
\(\Leftrightarrow\left(x-4\right)^2+\left(x-y\right)^2=0\)
Do: \(\left\{{}\begin{matrix}\left(x-4\right)^2\ge0\\\left(x-y\right)^2\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left(x-4\right)^2+\left(x-y\right)^2\ge0\)
Mặt khác: \(\left(x-4\right)^2+\left(x-y\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-4=0\\x-y=0\end{matrix}\right.\)
\(\Leftrightarrow x=y=4\)
Vậy: ...
bn giải giúp bài của mình ik ạ,c.ơn