Cho tam giác ABC vuông tại A hãy viết các tỉ số lượng giác của góc B
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VH
1
H9
HT.Phong (9A5)
CTVHS
24 tháng 10 2023
Các tỉ số lượng giác của góc B là:
\(\left\{{}\begin{matrix}sinB=\dfrac{AC}{BC}\\cosB=\dfrac{AB}{BC}\\tanB=\dfrac{AC}{AB}\\cotB=\dfrac{AB}{AC}\end{matrix}\right.\)
8 tháng 10 2021
\(a,\sin\widehat{C}=\dfrac{AB}{BC};\cos\widehat{C}=\dfrac{AC}{BC};\tan\widehat{C}=\dfrac{AB}{AC};\cot\widehat{C}=\dfrac{AC}{AB}\\ b,BC=\sqrt{AB^2+AC^2}=13\left(cm\right)\left(pytago\right)\\ \Rightarrow\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{12}{13};\cos\widehat{B}=\dfrac{AB}{BC}=\dfrac{5}{13}\\ \tan\widehat{B}=\dfrac{AC}{AB}=\dfrac{12}{5};\cot\widehat{B}=\dfrac{AB}{AC}=\dfrac{5}{12}\)
\(\tan\widehat{B}=\dfrac{AC}{AB}=\dfrac{12}{5}\approx\tan67^022'\\ \Rightarrow\widehat{B}\approx67^022'\\ \Rightarrow\widehat{C}=90^0-67^022'=22^038'\)
PT
1
PT
1
YD
0
H9
HT.Phong (9A5)
CTVHS
6 tháng 10 2023
Bài 1:
a) Ta có:
\(tanB=\dfrac{AC}{AB}\Rightarrow\dfrac{AC}{AB}=\dfrac{5}{2}\)
\(\Rightarrow AC=\dfrac{AB\cdot5}{2}=\dfrac{6\cdot5}{2}=15\)
b) Áp dụng Py-ta-go ta có:
\(BC^2=AB^2+AC^2=6^2+15^2=261\)
\(\Rightarrow BC=\sqrt{261}=3\sqrt{29}\)
H9
HT.Phong (9A5)
CTVHS
6 tháng 10 2023
Bài 2:
\(\left\{{}\begin{matrix}sinM=sin40^o\approx0,64\Rightarrow cosN\approx0,64\\cosM=cos40^o\approx0,77\Rightarrow sinN\approx0,77\\tanM=tan40^o\approx0,84\Rightarrow cotN\approx0,84\\cotM=cot40^o\approx1,19\Rightarrow tanN\approx1,19\end{matrix}\right.\)
DT
1
10 tháng 9 2019
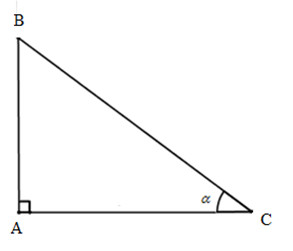
Vì tam giác ABC vuông tại A nên góc C nhọn. Vì thế:
sinC>0;cosC>0;tanC>0;cotC>0sinC>0;cosC>0;tanC>0;cotC>0
Vì hai góc B và C phụ nhau nên sinC = cosB = 0,8.
Ta có:
Sin2C+cos2C=1Sin2C+cos2C=1
⇒cos2C=1−sin2C=1−(0,8)2=0,36⇒cos2C=1−sin2C=1−(0,8)2=0,36
⇒cosC=0,6;⇒cosC=0,6;
tgC=sinCcosC=0,80,6=43;tgC=sinCcosC=0,80,6=43;
cotgC=cosCsinC=0,60,8=34
12 tháng 10 2021
a: \(\sin\widehat{B}=\cos\widehat{C}=\dfrac{AC}{BC}\)
\(\cos\widehat{B}=\sin\widehat{C}=\dfrac{AB}{BC}\)
\(\tan\widehat{B}=\cot\widehat{C}=\dfrac{AC}{AB}\)
\(\cot\widehat{B}=\tan\widehat{C}=\dfrac{AB}{AC}\)
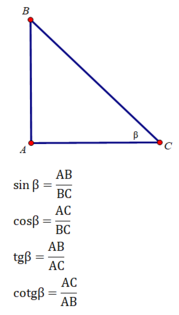
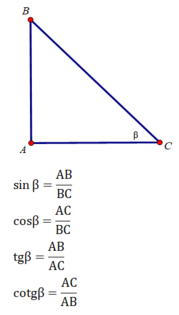
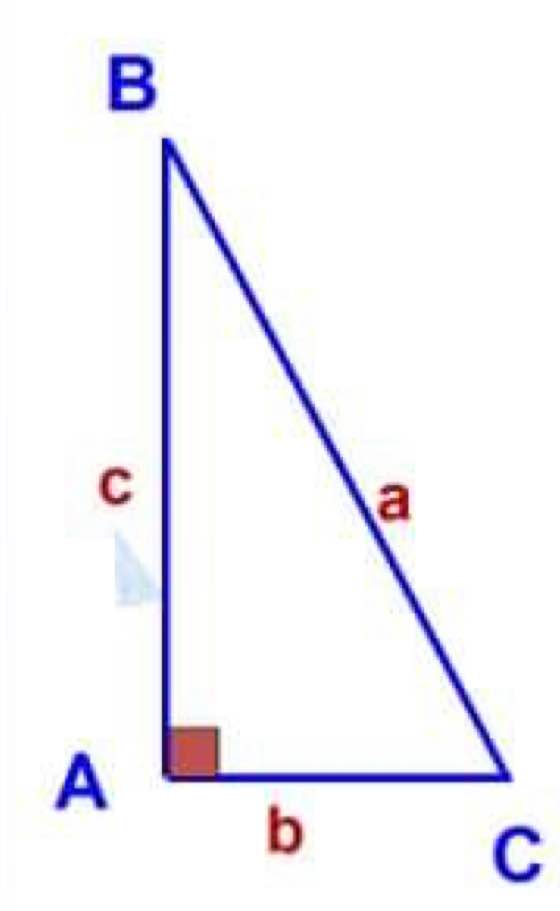
Các tỉ số lượng giác của góc B là:
\(\left\{{}\begin{matrix}sinB=\dfrac{\text{đối}}{\text{huyền}}\\cosB=\dfrac{\text{kề}}{\text{huyền}}\\tanB=\dfrac{\text{đối}}{\text{kề}}\\cotB=\dfrac{\text{kề}}{\text{đối}}\end{matrix}\right.\)
Các tỉ số lượng giác của góc B:
\(sinB=\dfrac{AC}{BC}\)
\(cosB=\dfrac{AB}{BC}\)
\(tanB=\dfrac{AC}{AB}\)
\(cotB=\dfrac{AB}{AC}\)