Question

[gấu béo]

   Tại một nơi ngang thuộc bằng mực nước biển, ở nhiệt độ bằng 10^oC, một đồng hồ quả lắc trong một ngày đêm chạy nhanh 6,48 giây. Coi con lắc đồng hồ như một con lắc đơn, thanh treo con lắc hệ số nở dài \(\alpha=2.10^{-5}.K^{-1}\)

a) Tại vị trí nói trên, ở nhiệt độ nào thì đồng hồ chạy đúng giờ

b) Đưa con lắc lên đỉnh núi với nhiệt độ bằng 6^oC, ta thấy đồng hồ chạy đúng giờ. Tính độ cao của đỉnh núi so với mực nước biển (bán kính Trái Đất bằng 6400 km)

c) Đưa con lắc lò xo lên độ cao 3,2 km và ở nhiệt độ -5^oC. Để đồng hộ chạy đúng giờ thì phải thay đổi chiều dài con lắc như thế nào

Answer 1

[nguyễn thị hương giang]

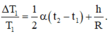
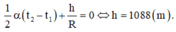
a)Gọi \(t_1\) là nhiệt độ đồng hồ chạy đúng.

Chu kì đồng hồ chạy đúng được xác định:

\(T_đ=T_1=2\pi\cdot\sqrt{\dfrac{l_1}{g_0}}=2\pi\cdot\sqrt{\dfrac{l_0\left(1+\alpha t_1\right)}{g_0}}\)

Khi nhiệt độ bằng \(10^oC\) thì chu kì đồng hồ chạy: 

\(T_s=T_2=2\pi\cdot\sqrt{\dfrac{l_2}{g_0}}=2\pi\cdot\sqrt{\dfrac{l_0\cdot\left(1+\alpha t_2\right)}{g_0}}\)

Đồng hồ chạy nhanh 6,48 giây nên \(T_1>T_2\)

\(\Rightarrow t_1=\dfrac{2\cdot6,48}{\alpha t}+t_2=\dfrac{2\cdot6,48}{2\cdot10^{-5}\cdot24\cdot3600}+10=17,5s\)

b)Con lắc chịu sự biến đổi của sự nở dài về nhiệt và sự thay đổi độ cao.

\(\dfrac{\Delta T_1}{T_1}=\dfrac{1}{2}\alpha\left(t_2-t_1\right)+\dfrac{h}{R}\)

Đồng hồ chạy đúng giờ: \(T_1=T_2\) và \(\Delta T=0\)

\(\Rightarrow\dfrac{1}{2}\alpha\left(t_2-t_1\right)+\dfrac{h}{R}=0\)

\(\Rightarrow\dfrac{1}{2}\cdot2\cdot10^{-5}\cdot\left(6-10\right)+\dfrac{h}{6400}=0\)

\(\Rightarrow h=0,256km=256m\)

c)Chu kì dao động của con lắc để đồng hồ chạy đúng:

\(\left\{{}\begin{matrix}T=2\pi\sqrt{\dfrac{l_0}{g}}\\T'=2\pi\sqrt{\dfrac{l_0\cdot\left(1+\alpha\cdot\Delta t\right)}{g'}}\end{matrix}\right.\)

\(\Rightarrow T=T'\Rightarrow\dfrac{l_0}{g}=\dfrac{l_0\left(1+\alpha.\Delta t\right)}{g'}\)

Gia tốc vật rơi tự do: \(g'=G\cdot\dfrac{M}{\left(R+h\right)^2}\)

\(\Rightarrow\dfrac{g'}{g}=\left(\dfrac{R}{R+h}\right)^2=1+\alpha.\Delta t\)

\(\Rightarrow\Delta t=\dfrac{\left(\dfrac{R}{R+h}\right)^2-1}{\alpha}=\dfrac{\left(\dfrac{6400}{6400+3,2}\right)^2-1}{2\cdot10^{-5}}\approx-50^oC=-58^oF\)

Chiều dài con lắc:

\(l=l_0\left(1+\alpha\Delta t\right)=3,2\cdot\left(1+2\cdot10^{-5}\cdot\left(-58\right)\right)=3,196288km\)