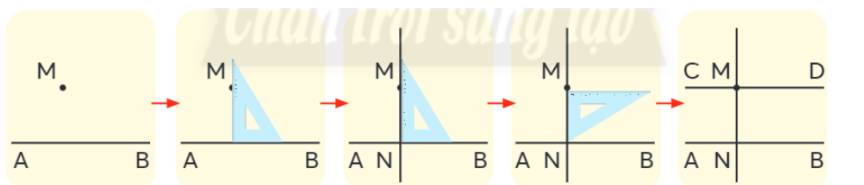
Cho trước đường thẳng AB và điểm M không nằm trên đường thẳng AB. Vẽ đường thẳng CD đi qua điểm M và song song với đường thẳng AB theo hướng dẫn sau:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
3 tháng 10 2023
1
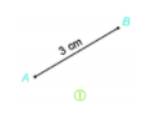
Bước 1. Vẽ đoạn thẳng AB = 3 cm.
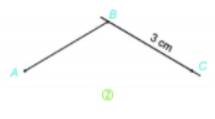
Bước 2. Vẽ đường thẳng đi qua B. Lấy điểm C trên đường thẳng đó sao cho BC = 3 cm.
Bước 3. Vẽ đường thẳng đi qua C và song song với cạnh AB. Vẽ đường thẳng đi qua A và song song với cạnh BC.
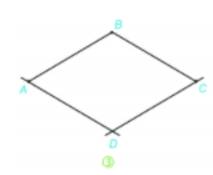
Bước 4. Hai đường thẳng này cắt nhau tại D, ta được hình thoi ABCD.
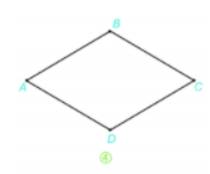
2. Em lấy thước thẳng đo được AB = BC = CD = DA = 3 cm. Vậy các cạnh của hình thoi ABCD vừa vẽ bằng nhau.
3.
Bước 1. Gấp đôi tờ giấy sau đó lại gấp đôi một lần nữa sao cho xuất hiện một góc vuông với cạnh là các nếp gấp.
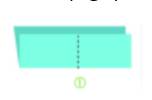
Bước 2. Vẽ một đoạn thẳng nối hai điểm tuỳ ý trên hai cạnh của góc vuông.
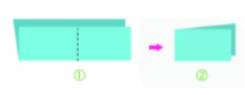
Bước 3. Dùng kéo cắt theo đoạn thẳng vừa vẽ rồi mở ra, ta được một hình thoi.
HQ
Hà Quang Minh
Giáo viên
3 tháng 10 2023
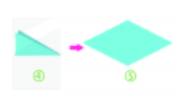
Bước 1. Vẽ đoạn thẳng AB = 5 cm.
Bước 2. Vẽ đường thẳng đi qua B. Trên đường thẳng đó lấy điểm C sao cho BC = 3 cm.
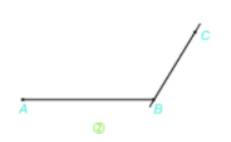
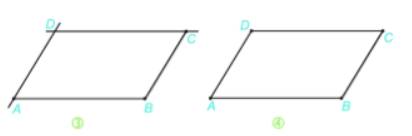
Bước 3. Vẽ đường thẳng đi qua A và song song với BC, đường thẳng qua C và song song với AB. Hai đường thẳng này cắt nhau tại D, ta được hình bình hành ABCD.
CM
3 tháng 5 2019
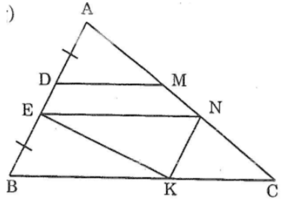
Từ N kẻ đường thẳng song song vói AB cắt BC tại K. Nối EK.
Xét ΔBEK và Δ NKE, ta có:
∠(EKB) =∠(KEN) (so le trong vì EN // BC)
EK cạnh chung
∠(BEK) =∠(NKE) (so le trong vì NK // AB))
Suy ra: Δ BEK = Δ NKE(g.c.g)
Suy ra: BE = NK (hai cạnh tương ứng)
EN = BK (hai cạnh tương ứng)
Xét Δ ADM và Δ NKC, ta có:
∠A =∠(KNC) (đồng vị vì NK // AB)
AD = NK ( vì cùng bằng BE)
∠(ADM) =∠(NKC) (vì cùng bằng góc B)
Suy ra: Δ ADM = Δ NKC(g.c.g)
Suy ra: DM = KC (hai cạnh tương ứng)
Mà BC = BK + KC. Suy ra: BC = EN + DM
PT
1
CM
24 tháng 8 2019
- Vẽ đường thẳng MN đi qua M và vuông góc với CD
- Vẽ đường thẳng AB đi qua M và vuông góc với MN
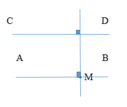
- Vẽ đường thẳng đi qua M và vuông góc với đường thẳng AB
- Vẽ đường thẳng CD đi qua M và vuông góc với đường thẳng vừa vẽ