Từ điểm A ở ngoài đường tròn (O;R), vẽ hai tiếp tuyến AB,AC với đường tròn (B,C là hai tiếp điểm). Gọi H là giao điểm OA và BC. Qua A ke dg vuong goc voi AB cat OC tai E.F la trung diem OB CM: 1. tg ABOC nt va xac dinh tam I cua dg tron ngoai tiep tg do2. CM: a) tam giac AOE can b) IF.IO=IE.OF3. Q la giao cua EF va BC. M la giao cua AC va IECM: AK vuong goc voi EF va O,Q,M thang...
Đọc tiếp
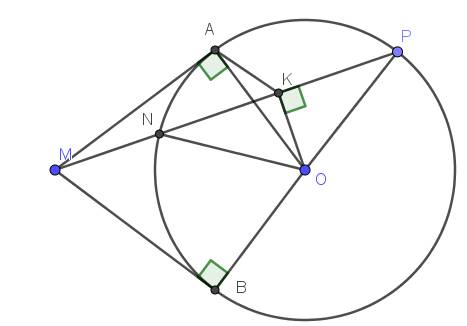
Từ điểm A ở ngoài đường tròn (O;R), vẽ hai tiếp tuyến AB,AC với đường tròn (B,C là hai tiếp điểm). Gọi H là giao điểm OA và BC. Qua A ke dg vuong goc voi AB cat OC tai E.F la trung diem OB CM:
1. tg ABOC nt va xac dinh tam I cua dg tron ngoai tiep tg do
2. CM: a) tam giac AOE can
b) IF.IO=IE.OF
3. Q la giao cua EF va BC. M la giao cua AC va IE
CM: AK vuong goc voi EF va O,Q,M thang hang
1: Xét tứ giác ABOC có
\(\widehat{OBA}\) và \(\widehat{OCA}\) là hai góc đối
\(\widehat{OBA}+\widehat{OCA}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ABOC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
2:
a) Cm ΔAOE cân tại E
Xét (O) có
AB là tiếp tuyến có B là tiếp điểm(gt)
AC là tiếp tuyến có C là tiếp điểm(gt)
Do đó: OA là tia phân giác của \(\widehat{BOC}\)(Tính chất hai tiếp tuyến cắt nhau)
\(\Leftrightarrow\widehat{BOA}=\widehat{COA}\)
mà \(\widehat{BOA}+\widehat{BAO}=90^0\)(ΔBOA vuông tại B)
nên \(\widehat{COA}=\widehat{BAO}\)
\(\Leftrightarrow\widehat{EOA}=\widehat{BAO}\)
mà \(\widehat{BAO}+\widehat{EAO}=90^0\)
nên \(\widehat{EOA}=\widehat{EAO}\)
Xét ΔEOA có \(\widehat{EOA}=\widehat{EAO}\)(cmt)
nên ΔEOA cân tại E(Định lí đảo của tam giác cân)