Bài 1 : biết các chữ số a,b thỏa mãn a7b.b=5211 Khi đó a.b=......
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HF
1
14 tháng 10 2023
\(\overline{ab4}-ab=319\)
\(\Leftrightarrow\overline{ab}.10+4-\overline{ab}=319\)
\(\Leftrightarrow\overline{ab}.9+4=319\)
\(\Leftrightarrow\overline{ab}.9=315\)
\(\Leftrightarrow\overline{ab}=35\)
Vậy \(a=3,b=5\)
\(\Rightarrow b-a=5-3=2\)
HF
3
KV
14 tháng 10 2023
a2b.b = 2556
⇒ b = 4 hoặc b = 6
TH1: b = 4
Ta có:
a24.4 = 2556
⇒ a24 = 2556 : 4
⇒ a24 = 639
⇒ 100a + 24 = 639
⇒ 100a = 639 - 24
⇒ 100a = 615
⇒ a = 615 : 100
⇒ a = 6,15 (loại)
TH2: a = 6
Ta có:
a26.6 = 2556
⇒ a26 = 2556 : 6
⇒ a26 = 426
⇒ 100a + 26 = 426
⇒ 100a = 426 - 26
⇒ 100a = 400
⇒ a = 400 : 100
⇒ a = 4 (nhận)
Vậy ab = 46
14 tháng 10 2023
\(\overline{a2b}.b=2556\)
\(\Rightarrow\left(a.100+2.10+b\right).b=2556\)
\(\Leftrightarrow a.b.100+2.10.b+b^2=2556\)
\(\Rightarrow\overline{...0}+\overline{...0}+b^2=2556\)
\(\Leftrightarrow\overline{...0}+b^2=2556\)
\(\Rightarrow b^2=2556-\overline{...0}\)
\(\Leftrightarrow b^2=\overline{...6}\)
Mà b là số tự nhiên có 1 chữ số,b2 có chữ số tận cùng là 6
\(\Rightarrow0\le b\le9\)
\(\Rightarrow0\le b^2\le81\)
\(\Rightarrow b^2=36\)
\(\Rightarrow b=6\)
Thay vào ta được:
\(a.6.100+2.10.6+36=2556\)
\(\Leftrightarrow a.600+120+36=2556\)
\(\Leftrightarrow a.600+156=2556\)
\(\Leftrightarrow a.600=2556-156\)
\(\Leftrightarrow a.600=2400\)
\(\Rightarrow a=2400:600=4\)
\(\Rightarrow a=4,b=6\)
Vậy \(ab=4.6=24\)
CM
26 tháng 12 2019
Đáp án A
Ta có
z − 1 = 1 ⇔ a − 1 + b i = 1 ⇔ a − 1 2 + b 2 = 1 1 .
Số phức
w = 1 + i z ¯ − 1 = 1 + i a − 1 − b i = a + b − 1 + a − b − 1 i
có phần số thực bằng a + b − 1 = 1 2 .
⇒ 1 , 2 ⇒ a − 1 2 + b 2 = 1 a + b = 2 ⇔ a + b = 2 b = 0 b = 1 ⇒ b = 1 a = 1 ⇒ a . b = 1.
CM
7 tháng 9 2019
Đáp án C
Phương pháp
Gọi số phức đã cho có dạng 
. Sử dụng giả thiết để đưa ra một hệ cho a, b giải trực tiếp hệ này để tìm a, b
Lời giải chi tiết.
Ta có: 
Do z không là số thực nên ta phải có b ≠ 0 (2)
Ta lại có
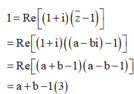
Từ (1), (2), (3) ta có hệ
CM
5 tháng 2 2019
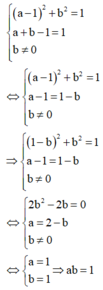
Đáp án A
Ta có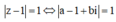 
Số phức 
có phần số thực bằng a+b-1 = 1(2)
Từ (1), (2)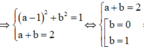 
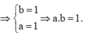
MM
5
24 tháng 1 2017
Khi đó a có giá trị lớn nhất là 0
b có giá trị lớn nhất là 1
Khi đó a.b có giá trị là 0.1=0
Vạy giá trị lớn nhất của a.b là 0.
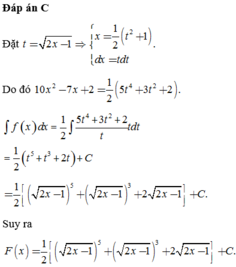
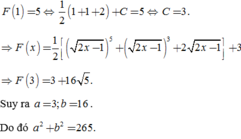
\(\overline{a7b}.b=5211\)
\(\Leftrightarrow\left(a.100+7.10+b\right).b=5211\)
\(\Leftrightarrow a.b.100+7.10.b+b^2=5211\)
\(\Rightarrow\overline{...0}+\overline{...0}+b^2=5211\)
\(\Leftrightarrow\overline{...0}+b^2\)
\(\Leftrightarrow b^2=5211-\overline{...0}\)
\(\Leftrightarrow b^2=\overline{...1}\)
Mà \(0\le b\le9\),\(b^2\) có chữ số tận cùng là 1
\(\Rightarrow0\le b^2\le81\)
\(\Rightarrow b^2=81\)
\(\Rightarrow b=9\)
Thay vào ta được:
\(a.9.100+7.10.9+81=5211\)
\(\Leftrightarrow a.900+630+81=5211\)
\(\Leftrightarrow a.900+711=5211\)
\(\Leftrightarrow a.900=5211-711\)
\(\Leftrightarrow a.900=4500\)
\(\Rightarrow a=5\)
Vậy a=5,b=9
\(\Rightarrow a.b=5.9=45\)
sossss