Cho hthang cân ABCD có AB//CD . Lấy M và N lần lượt là trung điểm của CD và AB. Cmr:
a) AM=BM
b)MN=DC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 7 2023
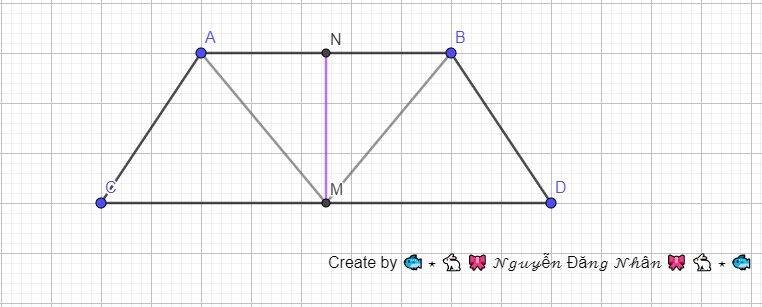
a) Xét 2 tam giác AMC và BMD có:
\(\widehat{C}=\widehat{D}\) (góc kề một đáy)
\(AC=BD\) (cạnh bên)
\(MC=MD\) (giả thiết)
\(\Rightarrow\Delta AMC=\Delta BMC\) (cạnh.góc.cạnh)
\(\Rightarrow AM=BM\)
b) Xét 2 tam giác NMA và NMB có:
\(NA=NB\) (giả thiết)
\(NM\): cạnh chung
\(MA=MB\) (chứng minh trên)
\(\Rightarrow\Delta NMA=\Delta NMB\)
\(\Rightarrow\widehat{MNA}=\widehat{MNB}\)
Mà 2 góc \(\widehat{MNA}=\widehat{MNB}\) là 2 góc kề bù, nên:
\(\widehat{MNA}=\widehat{MNB}=\dfrac{180^o}{2}=90^o\)
Vậy MN là đường cao:
29 tháng 10 2021
a: Xét tứ giác BMDN có
BM//DN
BM=DN
Do đó: BMDN là hình bình hành
22 tháng 6 2023
a: Xét ΔADM và ΔBCM có
AD=BC
góc ADM=góc BCM
DM=CM
=>ΔADM=ΔBCM
=>MA=MB
b: ΔMAB cân tại M
mà MN là đường trung tuyến
nên MN vuông góc AB
14 tháng 12 2017
BÀI 1: Gọi I là giao điểm của EF và AB
Vì EF là đường trung trực của MB nên BE = BF
Xét hai tam giác BEI và BFI thì chúng bằng nhau ( t.hợp ch-cgv)
=> IE = IF; EF vuông góc AB
=> E và F đối xứng nhau qua AB
* xét tứ giác MEBF có :
- EM = EB; FM = FB ( È là đường trung trực của MB)
mà E và F đối xứng nhau qua AB nên ta c/m được hai tam giác BEI và BFI bằng nhau ( t.hợp ch-cgv)
=> EM = EB = FM = FB
=> MEBF là hình thoi
*Vì EB // NC nên EBCN là hình thang có 2 đáy là EB và NC
để EBCN là hình thang cân thì EN = BC
H
22 tháng 8 2023
.a.
Vì `EF` là đường trung trực MB.
=> `EM=EB`
=> `ΔEMB` cân tại E
=> \(\widehat{EMB}=\widehat{EBM}\)
Chứng minh tương tự được: \(\widehat{FMB}=\widehat{FBM}\)
Vì `AM=DN` mà AM//DN
=> Tứ giác `AMND` là hình bình hành.
b.
Từ câu (a) suy ra:
ME//BF
BE//FM
=> Hình bình hành MEBF có `EF⊥MB`
=> Tứ giác MEBF là hình thoi