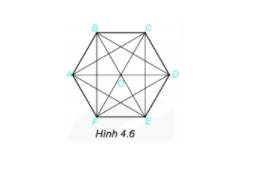
Cho hình lục giác đều như hình 4.6.
Ta đã biết, 6 tam giác đều ghép lại thành hình lục giác đều, đó là những tam giác đều nào? Ngoài 6 tam giác đều đó, trong hình em còn thấy những tam giác đều nào khác?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình vuông là b), tam giác đều là c), lục giác đều là g).
Hình vuông là a), tam giác đều là d), lục giác đều là e).
Hình vuông là b), tam giác đều là d), lục giác đều là e).
Hình vuông là a), tam giác đều là c), lục giác đều là g).

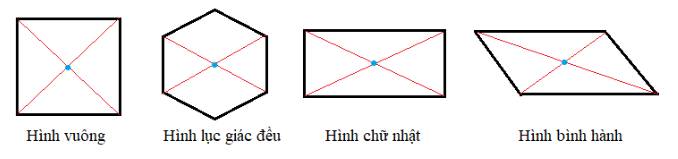
- Tâm đối xứng của hình vuông là giao điểm của hai đường chéo.
- Tâm đối xứng của hình lục giác đều là giao điểm của các đường chéo chính.
- Tâm đối xứng của hình chữ nhật là giao điểm của hai đường chéo.
- Tâm đối xứng của hình bình hành là giao điểm của hai đường chéo.
Các hình không có tâm đối xứng: Tam giác đều, hình thang cân.

| Chóp tam giác đều | Chóp tứ giác đều | Chóp ngũ giác đều | Chóp lục giác đều | |
| Đáy | Tam giác đều | Hình vuông | Ngũ giác đều | Lục giác đều |
| Mặt bên | Tam giác cân | Tam giác cân | Tam giác cân | Tam giác cân |
| Số cạnh đáy | 3 | 4 | 5 | 6 |
| Số cạnh | 6 | 8 | 10 | 12 |
| Số mặt | 4 | 5 | 6 | 7 |

1m
Do mỗi cạnh ở mỗi chậu hoa đều tạo thành 1 cạnh của hình lục giác mà mỗi cạnh của chậu hoa dài 1m => cạnh của hình lục giác đó là 1m

Hình vuông là hình b
Hình tam giác đều là hình c
Hình lục giác đều là hình g

Tam giác đều và ngũ giác dều không có tâm đối xứng.
* Hình bình hành có một tâm đối xứng là giao điểm của hai đường chéo.
* Hình lục giác đều có một tâm đối xứng, đó là tâm đường tròn ngoại tiếp hình lục giác đều.
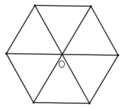

Hình bình hành và lục giác đều là những hình có tâm đối xứng.
Các tam giác đều ghép thành hình lục giác đều là: tam giác ABO, tam giác BCO, tam giác CDO, tam giác DEO, tam giác EFO, tam giác FAO.
Trong hình còn có các tam giác đều: ACE, BDF.