Một hệ dao động điều hoà với chu kì 1 s. Chọn gốc thế năng tại vị trí cân bằng của vật. Thời điểm hệ bắt đầu dao động thì động năng và thế năng bằng nhau lần thứ nhất. Hỏi sau bao lâu kể từ khi hệ bắt đầu dao động, động năng và thế năng bằng nhau lần thứ ba?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
5 tháng 11 2023
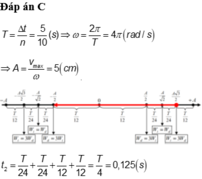
Hệ dao động điều hoà với chu kì 2 s nên tần số góc là: ω=π(rad/s)
Động năng và thế năng bằng nhau lần thứ nhất thì:
Wt=Wd⇒\(\frac{1}{2}\)mω2A2cos2(ωt+φ0)= \(\frac{1}{2}\)mω2A2sin2(ωt+φ0)
⇒cos2(πt+φ0)=sin2(πt+φ0)
⇒πt+φ0=\(\frac{\pi }{4} + \frac{{k\pi }}{2}\)
Lần thứ nhất động năng và thế năng bằng nhau nên k=1,t=0 nên ta có: φ0=\(\frac{{3\pi }}{4}\)
Động năng và thế năng bằng nhau lần thứ hai sau khoảng thời gian:
πt+\(\frac{{3\pi }}{4}\)=\(\frac{\pi }{4} + \frac{{2\pi }}{2}\)⇒t=0,5s
HQ
Hà Quang Minh
Giáo viên
27 tháng 8 2023
Phương trình dao động của vật là: \(x=Acos\left(\omega t-\dfrac{\pi}{2}\right)\)
Thế năng của dao động là: \(W_t=\dfrac{1}{2}m\omega^2A^2cos^2\left(\omega t-\dfrac{\pi}{2}\right)\)
Động năng của dao động là: \(W_d=\dfrac{1}{2}m\omega^2A^2sin^2\left(\omega t-\dfrac{\pi}{2}\right)\)
Đường màu xanh lá cây là thế năng, đường màu xanh nước biển là động năng
Trên đồ thị những thời điểm mà hai đồ thị cắt nhau thì động năng và thế năng có độ lớn bằng nhau
27 tháng 8 2023
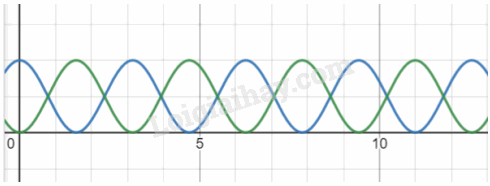
a) thế năng tăng dần trong khi động năng giảm dần là quá trình vật dao động từ vị trí cân bằng về hai biên.
b) thế năng giảm dần trong khi động năng tăng dần là quá trình vật dao động từ vị trí biên về vị trí cân bằng.
VT
26 tháng 6 2019
Đáp án B
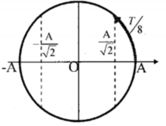
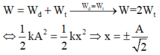
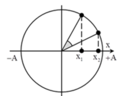
* Như vậy động năng bằng thế năng tại những vị trí x = ± A 2 và sau những thời gian cách đều là T/4.
* Dựa vào VTLG ta có thời gian cần tìm:
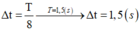
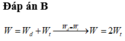
`W_[đ]=W_[t]=>W=2W_t`
`<=>1/2 kA^2=2. 1/2kx^2`
`<=>x=[+-\sqrt{2}A]/2`.
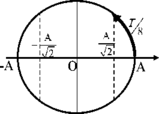
Dựa vào trục thời gian ta có: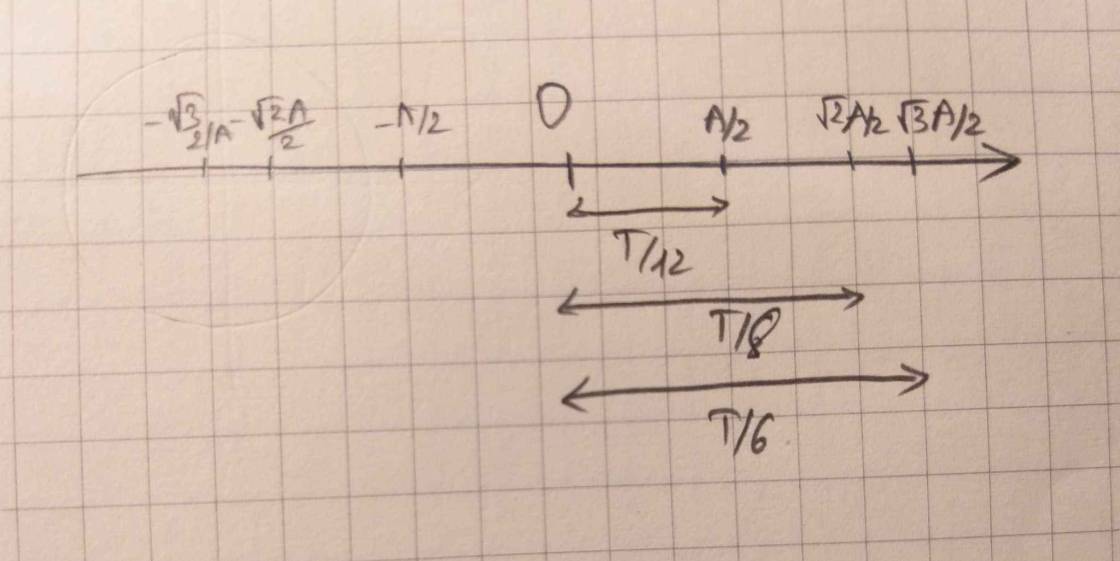
`=>t=T/4+T/4=[3T]/8=3/8(s)`.