Giải các bất phương trình sau:
a) \(7{x^2} - 19x - 6 \ge 0\)
b) \( - 6{x^2} + 11x > 10\)
c) \(3{x^2} - 4x + 7 > {x^2} + 2x + 1\)
d) \({x^2} - 10x + 25 \le 0\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,0,1^{2-x}>0,1^{4+2x}\\ \Leftrightarrow2-x>2x+4\\ \Leftrightarrow3x< -2\\ \Leftrightarrow x< -\dfrac{2}{3}\)
\(b,2\cdot5^{2x+1}\le3\\ \Leftrightarrow5^{2x+1}\le\dfrac{3}{2}\\ \Leftrightarrow2x+1\le log_5\left(\dfrac{3}{2}\right)\\ \Leftrightarrow2x\le log_5\left(\dfrac{3}{2}\right)-1\\ \Leftrightarrow x\le\dfrac{1}{2}log_5\left(\dfrac{3}{2}\right)-\dfrac{1}{2}\\ \Leftrightarrow x\le log_5\left(\dfrac{\sqrt{30}}{10}\right)\)
c, ĐK: \(x>-7\)
\(log_3\left(x+7\right)\ge-1\\ \Leftrightarrow x+7\ge\dfrac{1}{3}\\ \Leftrightarrow x\ge-\dfrac{20}{3}\)
Kết hợp với ĐKXĐ, ta có:\(x\ge-\dfrac{20}{3}\)
d, ĐK: \(x>\dfrac{1}{2}\)
\(log_{0,5}\left(x+7\right)\ge log_{0,5}\left(2x-1\right)\\ \Leftrightarrow x+7\le2x-1\\ \Leftrightarrow x\ge8\)
Kết hợp với ĐKXĐ, ta được: \(x\ge8\)

a) Ta có \(a = 2 > 0\) và \(\Delta = {\left( { - 5} \right)^2} - 4.2.3 = 1 > 0\)
=> \(2{x^2} - 5x + 3 = 0\) có 2 nghiệm phân biệt \({x_1} = 1,{x_2} = \frac{3}{2}\).
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \(2{x^2} - 5x + 3\) mang dấu “+” là \(\left( { - \infty ;1} \right) \cup \left( {\frac{3}{2}; + \infty } \right)\)
Vậy tập nghiệm của bất phương trình \(2{x^2} - 5x + 3 > 0\) là \(\left( { - \infty ;1} \right) \cup \left( {\frac{3}{2}; + \infty } \right)\)
b) Ta có \(a = - 1 < 0\) và \(\Delta ' = {\left( { - 1} \right)^2} - \left( { - 1} \right).8 = 9 > 0\)
=> \( - {x^2} - 2x + 8 = 0\)có 2 nghiệm phân biệt \({x_1} = - 4,{x_2} = 2\).
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \( - {x^2} - 2x + 8\) mang dấu “-” là \(\left( { - \infty ; - 4} \right] \cup \left[ {2; + \infty } \right)\)
Vậy tập nghiệm của bất phương trình \( - {x^2} - 2x + 8 \le 0\) là \(\left( { - \infty ; - 4} \right] \cup \left[ {2; + \infty } \right)\)
c)
Ta có \(a = 4 > 0\) và \(\Delta ' = {\left( { - 6} \right)^2} - 4.9 = 0\)
=> \(4{x^2} - 12x + 9 = 0\) có nghiệm duy nhất \(x = \frac{3}{2}\).
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \(4{x^2} - 12x + 9\) mang dấu “-” là \(\emptyset \)
Vậy tập nghiệm của bất phương trình \(4{x^2} - 12x + 9 < 0\) là \(\emptyset \)
d) \( - 3{x^2} + 7x - 4 \ge 0\)
Ta có \(a = - 3 < 0\) và \(\Delta = {7^2} - 4.\left( { - 3} \right).\left( { - 4} \right) = 1 > 0\)
=> \( - 3{x^2} + 7x - 4 = 0\) có 2 nghiệm phân biệt \({x_1} = 1;{x_2} = \frac{4}{3}\).
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \( - 3{x^2} + 7x - 4\) mang dấu “+” là \(\left[ {1;\frac{4}{3}} \right]\)
Vậy tập nghiệm của bất phương trình \( - 3{x^2} + 7x - 4 \ge 0\) là \(\left[ {1;\frac{4}{3}} \right]\)

a) Tam thức bậc hai \(f\left( x \right) = 2{x^2} - 15x + 28\) có hai nghiệm phân biệt là \({x_1} = \frac{7}{2};{x_2} = 4\)
và có \(a = 2 > 0\) nên \(f\left( x \right) \ge 0\) khi x thuộc hai nửa khoảng \(\left( { - \infty ;\frac{7}{2}} \right];\left[ {4; + \infty } \right)\)
Vậy tập nghiệm của bất phương trình \(2{x^2} - 15x + 28 \ge 0\) là \(\left( { - \infty ;\frac{7}{2}} \right] \cup \left[ {4; + \infty } \right)\)
b) Tam thức bậc hai \(f\left( x \right) = - 2{x^2} + 19x + 255\) có hai nghiệm phân biệt là \({x_1} = - \frac{{15}}{2};{x_2} = 17\)
và có \(a = - 2 < 0\) nên \(f\left( x \right) > 0\) khi x thuộc khoảng \(\left( { - \frac{{15}}{2};17} \right)\)
Vậy tập nghiệm của bất phương trình \( - 2{x^2} + 19x + 255 > 0\) là \(\left( { - \frac{{15}}{2};17} \right)\)
c) \(12{x^2} < 12x - 8 \Leftrightarrow 12{x^2} - 12x + 8 < 0\)
Tam thức bậc hai \(f\left( x \right) = 12{x^2} - 12x + 8\) có \(\Delta = - 240 < 0\) và \(a = 12 > 0\)
nên \(f\left( x \right) = 12{x^2} - 12x + 8\) dương với mọi x
Vậy bất phương trình \(12{x^2} < 12x - 8\) vô nghiệm
d) \({x^2} + x - 1 \ge 5{x^2} - 3x \Leftrightarrow -4{x^2} + 4x - 1 \ge 0\)
Tam thức bậc hai \(f\left( x \right) = -4{x^2} + 4x - 1\) có \(\Delta = 4^2 - 4.(-4).(-1)\)
Do đó tam thức bậc hai có nghiệm kép \({x_1} = {x_2}= \frac{1}{2}\) và a = - 4 < 0
Vậy bất phương trình \({x^2} + x - 1 \ge 5{x^2} - 3x\) có tập nghiệm S = {\(\frac{1}{2}\)}

a) ( 3.x + 1 ) . ( 7.x + 3 ) = (5.x-7 ) . ( 3.x + 1 )
<=> ( 3.x + 1 ) . ( 7.x + 3 ) - ( 5.x - 7) . ( 3.x + 1 ) = 0
<=> ( 3.x + 1 ) . ( 7.x + 3 - 5.x + 7 ) = 0
<=> ( 3.x + 1 ) . ( 2.x + 10 ) = 0
<=> \(\orbr{\begin{cases}3.x+1=0\\2.x+10=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{-1}{3}\\x=-5\end{cases}}}\)
Vậy x = { \(\frac{-1}{3};-5\)}
b) x2 + 10.x + 25 - 4.x . ( x + 5 ) = 0
<=> ( x + 5 )2 -4.x . (x + 5 ) = 0
<=> ( x+ 5 ) . ( x + 5 - 4.x ) = 0
<=> ( x + 5 ) . ( 5 - 3.x ) = 0
<=> \(\orbr{\begin{cases}x+5=0\\5-3.x\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-5\\x=\frac{5}{3}\end{cases}}}\)
Vậy x = \(\left\{\frac{5}{3};-5\right\}\)
c) (4.x - 5 )2 - 2. ( 16.x2 -25 ) = 0
<=> ( 4.x-5)2 -2 .( 4.x-5) .( 4.x + 5 ) = 0
<=> ( 4.x -5 )2 - ( 8.x+ 10 ) . ( 4.x -5 ) = 0
<=> ( 4.x -5 ) . ( 4.x-5 - 8.x - 10 ) = 0
<=> ( 4.x - 5 ) . ( -4.x - 15 ) = 0
<=> \(\orbr{\begin{cases}4.x-5=0\\-4.x-15=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{5}{4}\\x=\frac{-15}{4}\end{cases}}}\)
Vậy x = \(\left\{\frac{5}{4};\frac{-15}{4}\right\}\)
d) ( 4.x + 3 )2 = 4. ( x2 - 2.x + 1 )
<=> 16.x2 + 24.x + 9 - 4.x2 + 8.x - 4 = 0
<=> 12.x2 + 32.x + 5 =0
<=> 12. ( x +\(\frac{1}{8}\) ) . ( x + \(\frac{5}{2}\)) = 0
<=> \(\orbr{\begin{cases}x+\frac{1}{6}=0\\x+\frac{5}{2}=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{-1}{6}\\x=\frac{-5}{2}\end{cases}}}\)
Vậy x = \(\left\{\frac{-1}{6};\frac{-5}{2}\right\}\)
e) x2 -11.x + 28 = 0
<=> x2 -4.x - 7.x + 28 = 0
<=> ( x - 7 ) . ( x - 4 ) = 0
<=> \(\orbr{\begin{cases}x-7=0\\x-4=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=7\\x=4\end{cases}}}\)
Vậy x = { 4 ; 7 }
f ) 3.x.3 - 3.x2 - 6.x = 0
<=> 3.x. ( x2 -x - 2 ) = 0
<=> 3.x. ( x - 2 ) . ( x + 1 ) = 0
<=> \(\orbr{\begin{cases}x-2=0\\x+1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=2\\x=-1\end{cases}}}\)
\([x=0\) \([x=0\)
( Lưu ý :Lưu ý này không cần ghi vào vở : Chị nối 2 ý đó làm 1 nha cj ! )
Vậy x = { 2 ; -1 ; 0 }

a) \(2{x^2} + 3x + 1 \ge 0\)
Tam thức bậc hai \(f\left( x \right) = 2{x^2} + 3x + 1\) có 2 nghiệm phân biệt \(x = - 1,x = \frac{{ - 1}}{2}\)
hệ số \(a = 2 > 0\)
Ta có bảng xét dấu f(x) như sau:
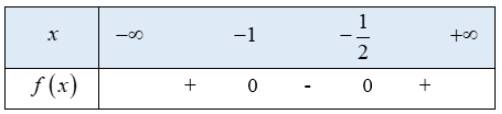
Từ bảng xét dấu ta thấy \(f\left( x \right) \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \le - 1\\x \ge - \frac{1}{2}\end{array} \right.\)
Vậy tập nghiệm của bất phương trình là \(\left( { - \infty ; - 1} \right] \cup \left[ { - \frac{1}{2}; + \infty } \right)\)
b) \( - 3{x^2} + x + 1 > 0\)
Tam thức bậc hai \(f\left( x \right) = - 3{x^2} + x + 1\) có 2 nghiệm phân biệt \(x = \frac{{1 - \sqrt {13} }}{6},x = \frac{{1 + \sqrt {13} }}{6}\)
Hệ số \(a = - 3 < 0\)
Ta có bảng xét dấu f(x) như sau:

Từ bảng xét dấu ta thấy \(f\left( x \right) > 0\)\( \Leftrightarrow \frac{{1 - \sqrt {13} }}{6} < x < \frac{{1 + \sqrt {13} }}{6}\)
Vậy tập nghiệm của bất phương trình là \(\left( {\frac{{1 - \sqrt {13} }}{6};\frac{{1 + \sqrt {13} }}{6}} \right)\)
c) \(4{x^2} + 4x + 1 \ge 0\)
Tam thức bậc hai \(f\left( x \right) = 4{x^2} + 4x + 1\) có nghiệm duy nhất \(x = \frac{{ - 1}}{2}\)
hệ số \(a = 4 > 0\)
Ta có bảng xét dấu f(x) như sau:

Từ bảng xét dấu ta thấy \(f\left( x \right) \ge 0 \Leftrightarrow x \in \mathbb{R}\)
Vậy tập nghiệm của bất phương trình là \(\mathbb{R}\)
d) \( - 16{x^2} + 8x - 1 < 0\)
Tam thức bậc hai \(f\left( x \right) = - 16{x^2} + 8x - 1\) có nghiệm duy nhất \(x = \frac{1}{4}\)
hệ số \(a = - 16 < 0\)
Ta có bảng xét dấu f(x) như sau:
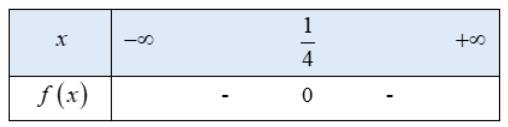
Từ bảng xét dấu ta thấy \(f\left( x \right) < 0 \Leftrightarrow x \ne \frac{1}{4}\)
Vậy tập nghiệm của bất phương trình là \(\mathbb{R}\backslash \left\{ {\frac{1}{4}} \right\}\)
e) \(2{x^2} + x + 3 < 0\)
Ta có \(\Delta = {1^2} - 4.2.3 = - 23 < 0\) và có \(a = 2 > 0\)
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \(2{x^2} + x + 3\) mang dấu “-” là \(\emptyset \)
Vậy tập nghiệm của bất phương trình \(2{x^2} + x + 3 < 0\) là \(\emptyset \)
g) \( - 3{x^2} + 4x - 5 < 0\)
Tam thức bậc hai \(f\left( x \right) = - 3{x^2} + 4x - 5\) có \(\Delta ' = {2^2} - \left( { - 3} \right).\left( { - 5} \right) = - 11 < 0\) và có \(a = - 3 < 0\)
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \( - 3{x^2} + 4x - 5\) mang dấu “-” là \(\mathbb{R}\)
Vậy tập nghiệm của bất phương trình \( - 3{x^2} + 4x - 5 < 0\) là \(\mathbb{R}\)

bạn phải phân tích đa thức thành nhân tử để hạ bậc. Một mẹo mình mách bạn thế này . bạn tìm một giá trị của x thỏa mãn thì dựa vào đó đó phân tich. Thông thường giá trị đó là ước của hằng số trong vế trái ví dụ câu a bạn thay ước của 12. mình thấy -1 thỏa mãn vậy khi phân tích đa thức thành nhân tử chắc chắn sẽ xuất hiện nhân tử là x+1 và dựa vào đó mình phân tích như sau:
x3-6x2+5x+12=0
<=> x3+x2-7x2-7x+12x+12=0
<=> (x3+x2)-(7x2+7x)+(12x+12)=0
<=> x2(x+1)-7x(x+1)+12(x+1)=0
<=> (x+1)(x2-7x+12)=0
Phân tích tiếp nhóm x2-7x+12 = x2-3x-4x+12 = x(x-3)-4(x-3) = (x-3)(x-4)
vậy phương trình tương đương
<=> (x+1)(x-3)(x-4) = 0
đến đây dễ dàng suy ra x = -1; 3; 4
Các câu còn lại tương tự bạn tự làm vì quá nhiều mình không gõ được

a) Ta có \(a = 3 > 0\) và tam thức bậc hai \(f\left( x \right) = 3{x^2} - 2x + 4\) có \(\Delta ' = {1^2} - 3.4 = - 11 < 0\)
=> \(f\left( x \right) = 3{x^2} - 2x + 4\) vô nghiệm.
=> \(3{x^2} - 2x + 4 > 0\forall x \in \mathbb{R}\)
b) Ta có: \(a = - 1 < 0\) và \(\Delta ' = {3^2} - \left( { - 1} \right).\left( { - 9} \right) = 0\)
=> \(f\left( x \right) = - {x^2} + 6x - 9\) có nghiệm duy nhất \(x = 3\).
=> \( - {x^2} + 6x - 9 < 0\forall x \in \mathbb{R}\backslash \left\{ 3 \right\}\)

a, (3x+1)(7x+3)=(5x-7)(3x+1)
<=> (3x+1)(7x+3)-(5x-7)(3x+1)=0
<=> (3x+1)(7x+3-5x+7)=0
<=> (3x+1)(2x+10)=0
<=> 2(3x+1)(x+5)=0
=> 3x+1=0 hoặc x+5=0
=> x= -1/3 hoặc x=-5
Vậy...
a) (3x - 2)(4x + 5) = 0
⇔ 3x - 2 = 0 hoặc 4x + 5 = 0
1) 3x - 2 = 0 ⇔ 3x = 2 ⇔ x = 2/3
2) 4x + 5 = 0 ⇔ 4x = -5 ⇔ x = -5/4
Vậy phương trình có tập nghiệm S = {2/3;−5/4}
b) (2,3x - 6,9)(0,1x + 2) = 0
⇔ 2,3x - 6,9 = 0 hoặc 0,1x + 2 = 0
1) 2,3x - 6,9 = 0 ⇔ 2,3x = 6,9 ⇔ x = 3
2) 0,1x + 2 = 0 ⇔ 0,1x = -2 ⇔ x = -20.
Vậy phương trình có tập hợp nghiệm S = {3;-20}
c) (4x + 2)(x2 + 1) = 0 ⇔ 4x + 2 = 0 hoặc x2 + 1 = 0
1) 4x + 2 = 0 ⇔ 4x = -2 ⇔ x = −1/2
2) x2 + 1 = 0 ⇔ x2 = -1 (vô lí vì x2 ≥ 0)
Vậy phương trình có tập hợp nghiệm S = {−1/2}
d) (2x + 7)(x - 5)(5x + 1) = 0
⇔ 2x + 7 = 0 hoặc x - 5 = 0 hoặc 5x + 1 = 0
1) 2x + 7 = 0 ⇔ 2x = -7 ⇔ x = −7/2
2) x - 5 = 0 ⇔ x = 5
3) 5x + 1 = 0 ⇔ 5x = -1 ⇔ x = −1/5
Vậy phương trình có tập nghiệm là S = {−7/2;5;−1/5}
a) Xét tam thức \(f\left( x \right) = 7{x^2} - 19x - 6\) có \(\Delta = 529 > 0\), có hai nghiệm phân biệt \({x_1} = - \frac{2}{7},{x_2} = 3\) và có \(a = 7 > 0\)
Ta có bảng xét dấu như sau
Vậy nghiệm của bất phương trình là đoạn \(\left[ { - \frac{2}{7};3} \right]\)
b) \( - 6{x^2} + 11x > 10 \Leftrightarrow - 6{x^2} + 11x - 10 > 0\)
Xét tam thức \(f\left( x \right) = - 6{x^2} + 11x - 10\) có \(\Delta = - 119 < 0\)và có \(a = - 6 < 0\)
Ta có bảng xét dấu như sau
Vậy bất phương trình vô nghiệm
c) \(3{x^2} - 4x + 7 > {x^2} + 2x + 1 \Leftrightarrow 2{x^2} - 6x + 6 > 0\)
Xét tam thức \(f\left( x \right) = 2{x^2} - 6x + 6\) có \(\Delta = - 12 < 0\)và có \(a = 2 > 0\)
Ta có bảng xét dấu như sau
Vậy bất phương trình có vô số nghiệm
d) Xét tam thức \(f\left( x \right) = {x^2} - 10x + 25\) có \(\Delta = 0\), có nghiệm kép \({x_1} = {x_2} = 5\) và có \(a = 1 > 0\)
Ta có bảng xét dấu như sau
Vậy nghiệm của bất phương trình là \(x = 5\)