Xét dấu tam thức bậc hai \(h\left( x \right) = - 0,006{x^2} + 1,2x - 30\) trong bài toán khởi động và cho biết ở khoảng cách nào tính từ đầu cầu O thì vòm cầu: cao hơn mặt cầu, thấp hơn mặt cầu
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
1 tháng 5 2019
Khi vận động viên ở độ cao 3m nghĩa là h =3m
Ta có: 3 = - x - 1 2 + 4 ⇔ x - 1 2 – 1=0 ⇔ x 2 – 2x = 0
⇔ x(x – 2) = 0 ⇔ x=0 hoặc x – 2 =0 ⇔ x = 0 hoặc x = 2
Vậy x = 0m hoặc x = 2m
CM
19 tháng 8 2018
Khi vận động viên chạm mặt nước nghĩa là h = 0m
Ta có: 0 = - x - 1 2 + 4 ⇔ x 2 -2x -3 =0
∆ ' = b ' 2 – ac = - 1 2 -1.(-3) =1 +3 = 4 > 0
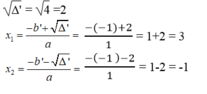
Vì khoảng cách không thể mang giá trị âm nên x=3m
CM
18 tháng 3 2017
Đáp án D
Từ vị trí tương đối của một mặt phẳng với mặt cầu ta có đáp án đúng là D.
21 tháng 6 2017
a) \(3=-\left(x-1\right)^2+4\Leftrightarrow x^2-2x=0\)
Suy ra \(x_1=0;x_2=2\)
b) Khi vận động viên chạm mặt nước thì \(h=0\).
Do đó \(-\left(x-1\right)^2+4=0\) hay \(x^2-2x-3=0\)
Suy ra \(x_1=-1;x_2=3\)
Vì khoảng cách không âm nên \(x_2=3\left(m\right)\)
CM
20 tháng 2 2019
Đáp án D
Ta có:
R = d 2 + M N 2 2 = 25 + 12 2 = 13 ⇒ S = 4 π R 2 = 676 π .
CM
11 tháng 3 2018
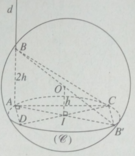
Diện tích tam giác BCD bằng:
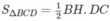
Diện tích này lớn nhất khi AI // CD.
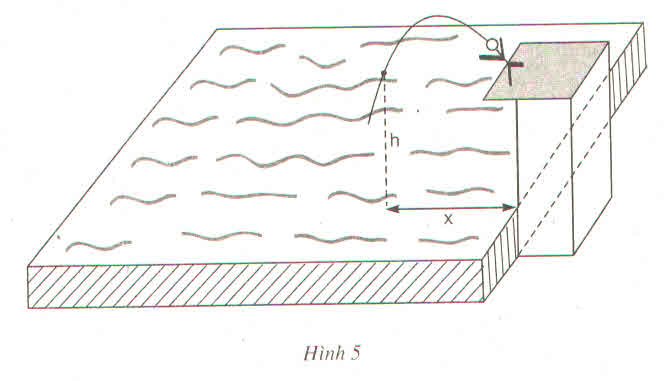
\(h\left( x \right) = - 0,006{x^2} + 1,2x - 30\) có \(\Delta = 1,{2^2} - 4.\left( { - 0,006} \right).\left( { - 30} \right) = \frac{{18}}{{25}} > 0\), hai nghiệm phân biệt là \({x_1} = 100 - 50\sqrt 2 ;{x_2} = 100 + 50\sqrt 2 \) và \(a = - 0,006 < 0\)
Ta có bảng xét dấu \(h\left( x \right)\) như sau:
Vậy vòm cầu cao hơn mặt cầu là khoảng cách từ \(100 - 50\sqrt 2 \)(m) đến \(100 + 50\sqrt 2 \) (m) (cách từ O), vòm vòm cầu thấp hơn mặt cầu là khoảng cách từ O đến\(100 - 50\sqrt 2 \)(m) và từ \(100 + 50\sqrt 2 \) (m) đến 200 (m) (cách từ O)