Hãy ước lượng sai số tương đối trong phép đo tuổi của vũ trụ và thời gian chạy của vận động viên ở Hoạt động khám phá 3.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
Ta có: \(\frac{{21}}{{13799}} = 0,0015...\) và \(\frac{{0,1}}{{10,3}} = 0,0097...\)
\( \Rightarrow \frac{{21}}{{13799}} < \frac{{0,1}}{{10,3}}\) hay phép đo ước lượng độ tuổi của vũ trụ có độ chính xác cao hơn.
QT
1
HQ
Hà Quang Minh
Giáo viên
27 tháng 9 2023
Từ câu b) của hoạt động khám phá 1, ta có không gian mẫu là
\( \begin{array}{l}\Omega =\{\left( {1;1} \right);\left( {1;2} \right);\left( {1;3} \right);\left( {1;4} \right);\left( {1;5} \right);\left( {1;6} \right);\left( {2;1} \right);\left( {2;2} \right);\left( {2;3} \right);\left( {2;4} \right);\left( {2;5} \right);\left( {2;6} \right);\left( {3;1} \right);\left( {3;2} \right);\\\left( {3;3} \right);\left( {3;4} \right);\left( {3;5} \right);\left( {3;6} \right);\left( {4;1} \right);\left( {4;2} \right);\left( {4;3} \right);\left( {4;4} \right);\left( {4;5} \right);\left( {4;6} \right);\\\left( {5;1} \right);\left( {5;2} \right);\left( {5;3} \right);\left( {5;4} \right);\left( {5;5} \right);\left( {5;6} \right);\left( {6;1} \right);\left( {6;2} \right);\left( {6;3} \right);\left( {6;4} \right);\left( {6;5} \right);\left( {6;6} \right)\}\end{array} \)
QT
Quoc Tran Anh Le
Giáo viên
10 tháng 12 2023
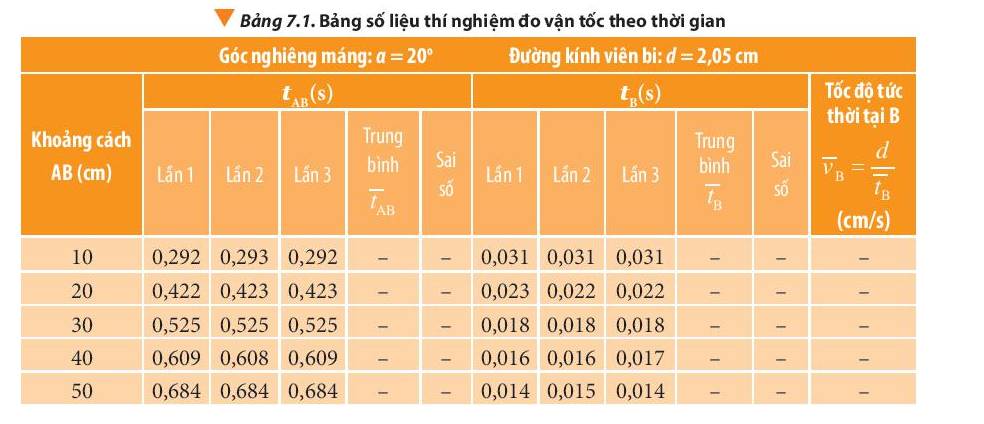
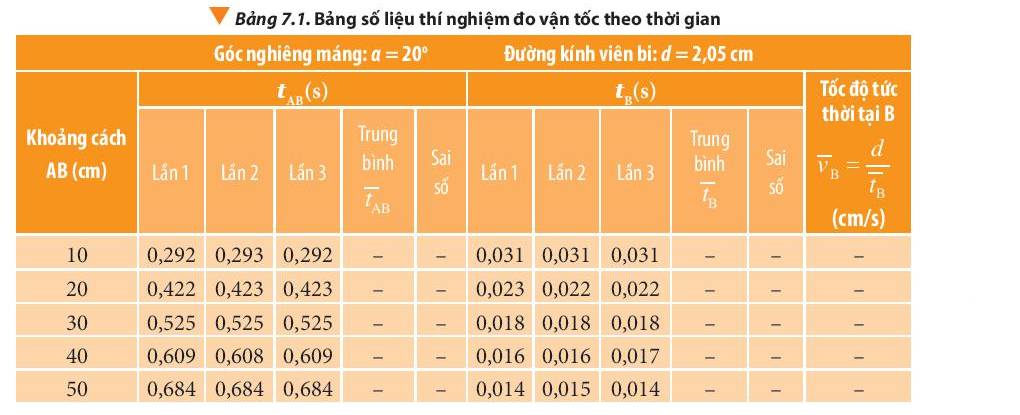
- Giá trị trung bình thời gian của viên bi chuyển động từ A đến B là:
+ AB = 10 cm: \(\overline t = \frac{{0,292 + 0,293 + 0,292}}{3} \approx 0,292(s)\)
+ AB = 20 cm: \(\overline t = \frac{{0,422 + 0,423 + 0,423}}{3} \approx 0,423(s)\)
+ AB = 30 cm: \(\overline t = \frac{{0,525 + 0,525 + 0,525}}{3} = 0,525(s)\)
+ AB = 40 cm: \(\overline t = \frac{{0,609 + 0,608 + 0,609}}{3} \approx 0,609(s)\)
+ AB = 50 cm: \(\overline t = \frac{{0,609 + 0,608 + 0,609}}{3} \approx 0,609(s)\)
- Sai số của phép đo thời gian viên bi chuyển động từ A đến B:
+ AB = 10 cm:
\(\begin{array}{l}\Delta {t_1} = \left| {0,292 - 0,292} \right| = 0\\\Delta {t_2} = \left| {0,293 - 0,292} \right| = 0,001\\\Delta {t_3} = \left| {0,292 - 0,292} \right| = 0\\ \Rightarrow \overline {\Delta t} = \frac{{0,001}}{3} \approx 3,{33.10^{ - 4}}(s)\end{array}\)
Tương tự cho các đoạn còn lại, ta có:
+ AB = 20 cm: \(\overline {\Delta t} = 3,{33.10^{ - 4}}(s)\)
+ AB = 30 cm: \(\overline {\Delta t} = 0\)
+ AB = 40 cm: \(\overline {\Delta t} = 3,{33.10^{ - 4}}(s)\)
+ AB = 50 cm: \(\overline {\Delta t} = 0\)
- Giá trị trung bình và sai số của thời gian chắn cổng quang điện tại B:
+ AB = 10 cm: \(\overline t = 0,031;\overline {\Delta t} = 0\)
+ AB = 20 cm: \(\overline t = 0,022;\overline {\Delta t} = 3,{33.10^{ - 4}}\)
+ AB = 30 cm: \(\overline t = 0,018;\overline {\Delta t} = 0\)
+ AB = 40 cm: \(\overline t = 0,016;\overline {\Delta t} = 3,{33.10^{ - 4}}\)
+ AB = 50 cm: \(\overline t = 0,014;\overline {\Delta t} = 3,{33.10^{ - 4}}\)
- Tốc độ tức thời tại B:
+ AB = 10 cm: \(\overline {{v_B}} = \frac{d}{{\overline {{t_B}} }} = \frac{{10}}{{0,031}} \approx 322,58(cm/s)\)
+ AB = 20 cm: \(\overline {{v_B}} = \frac{d}{{\overline {{t_B}} }} = \frac{{20}}{{0,022}} \approx 909,09(cm/s)\)
+ AB = 30 cm: \(\overline {{v_B}} = \frac{d}{{\overline {{t_B}} }} = \frac{{30}}{{0,018}} \approx 1666,67(cm/s)\)
+ AB = 40 cm: \(\overline {{v_B}} = \frac{d}{{\overline {{t_B}} }} = \frac{{40}}{{0,016}} = 2500(cm/s)\)
+ AB = 50 cm: \(\overline {{v_B}} = \frac{d}{{\overline {{t_B}} }} = \frac{{50}}{{0,014}} \approx 3571,43(cm/s)\)
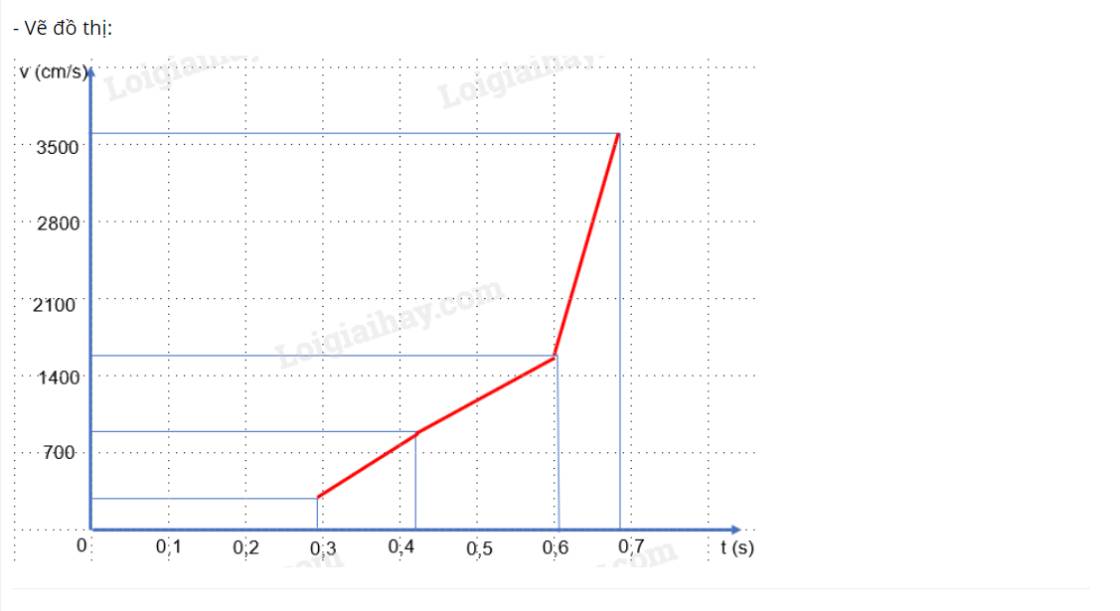
- Vẽ đồ thị:
24 tháng 5 2016
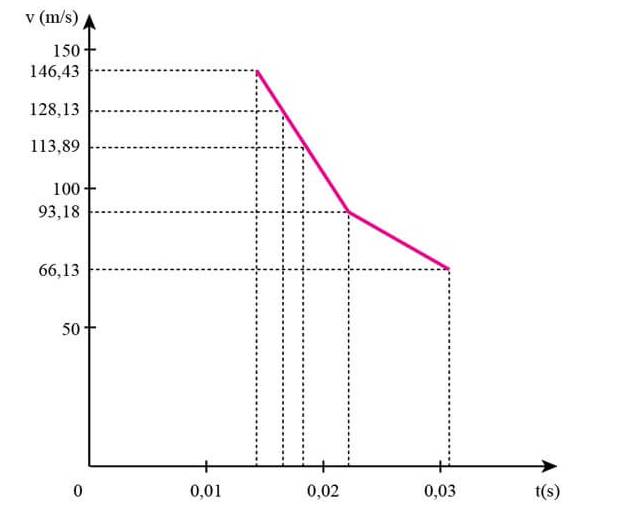
- Gọi vận tốc của vận động viên chạy và vận động viên đua xe đạp là: v1, v2 (v1> v2> 0). Khoảng cách giữa hai vận động viên chạy và hai vận động viên đua xe đạp là l1, l2 (l2>l1>0). Vì vận động viên chạy và vận động viên đua xe đạp chuyển động cùng chiều nên vận tốc của vận động viê đua xe khi chộn vận động viên chạy làm mốc là:
v21= v2 - v1 = 10 - 6 = 4 (m/s).
- Thời gian hai vận động viên đua xe vượt qua một vận động viên chạy là:
\(t_1=\frac{l_2}{v_{21}}=\frac{20}{4}=5\)(s)
- Thời gian một vận động viên đua xe đạp đang ở ngang hàng một vận động viên chạy đuổi kịp một vận động viên chạy tiếp theo là:
\(t_1=\frac{l_2}{v_{21}}=\frac{10}{4}=2,5\) (s)
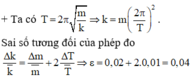
Trong phép đo tuổi của vũ trụ, ta có: \(d = 21;a = 13799\)
Sai số tương đối không vượt quá \(\frac{{21}}{{13799}} \approx 0,15\% \)
Trong phép đo thời gian chạy của vận động viên, ta có: \(d = 0,1;a = 10,3\)
Sai số tương đối không vượt quá \(\frac{{0,1}}{{10,3}} \approx 0,97\% \)