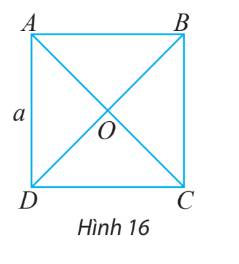
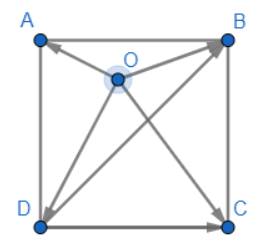
Cho hình vuông ABCD có tâm O và có các cạnh bằng a (hình 16)
a) Tìm trong hình hai vectơ bằng nhau và có độ dài bằng \(\frac{{a\sqrt 2 }}{2}\)
b) Tìm trong hình hai vectơ đối nhau và có độ dài bằng \(a\sqrt 2\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

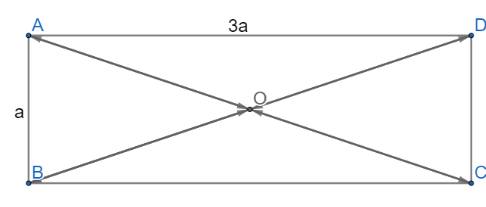
a) Ta có:
\(AC = BD = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {{\left( {3a} \right)}^2}} = a\sqrt {10} \)
+) \(\left| {\overrightarrow {AC} } \right| = AC = a\sqrt {10} \)
+) \(\left| {\overrightarrow {BD} } \right| = BD = a\sqrt {10} \)
b) O là giao điểm của hai đường chéo nên ta có:
\(AO = OC = BO = OD = \frac{{a\sqrt {10} }}{2}\)
Dựa vào hình vẽ ta thấy AO và CO cùng nằm trên một đường thẳng; BO và DO cùng nằm trên một đường thẳng
Suy ra các cặp vectơ đối nhau và có độ dài bằng \(\frac{{a\sqrt {10} }}{2}\) là:
\(\overrightarrow {OA} \) và \(\overrightarrow {OC} \); \(\overrightarrow {AO} \) và \(\overrightarrow {CO} \); \(\overrightarrow {OB} \) và \(\overrightarrow {OD} \); \(\overrightarrow {BO} \) và \(\overrightarrow {DO} \)

ABCD là hình vuông
\(\Rightarrow\Delta ABD\&\Delta ACD\) là tam vuông cân
\(\Rightarrow\left\{{}\begin{matrix}\left|\overrightarrow{AC}\right|=\left|\overrightarrow{AD}\right|.\sqrt[]{2}\\\left|\overrightarrow{BD}\right|=\left|\overrightarrow{AB}\right|.\sqrt[]{2}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left|\overrightarrow{AC}\right|=\dfrac{\sqrt[]{2}}{2}.\sqrt[]{2}=1\\\left|\overrightarrow{BD}\right|=\dfrac{\sqrt[]{2}}{2}.\sqrt[]{2}=1\end{matrix}\right.\)
\(\left|\overrightarrow{OA}\right|=\left|\overrightarrow{AO}\right|=\dfrac{1}{2}.\left|\overrightarrow{AC}\right|\) (O là trung điểm AC)
\(\Rightarrow\left|\overrightarrow{OA}\right|=\left|\overrightarrow{AO}\right|=\dfrac{1}{2}.1=\dfrac{1}{2}\)

Ta có: \(AC = BD = \sqrt {A{D^2} + D{C^2}} = \sqrt {{{\left( {\frac{{\sqrt 2 }}{2}} \right)}^2} + {{\left( {\frac{{\sqrt 2 }}{2}} \right)}^2}} = 1\)
\(OA = \frac{1}{2}AC = \frac{1}{2}\)
Suy ra: \(\left| {\overrightarrow {AC} } \right| = 1\), \(\left| {\overrightarrow {BD} } \right| = 1\), \(\left| {\overrightarrow {OA} } \right| = 1\), \(\left| {\overrightarrow {AO} } \right| = 1\)

Bằng \(\overrightarrow{AB}\) là \(\overrightarrow{DC}\)
Bằng \(\overrightarrow{OB}\) là \(\overrightarrow{DO}\)
Có độ dài bằng OB là \(\overrightarrow{OB};\overrightarrow{BO};\overrightarrow{OD};\overrightarrow{DO}\)
a) Bằng vectơ AB :
\(\overrightarrow{DC}\)
Bằng vectơ OB :
\(\overrightarrow{DO}\)
b)Có độ dài bằng OB :
\(\overrightarrow{OD},
\overrightarrow{DO},
\overrightarrow{BO}\)

a) I là tâm của ABCD, suy ra \(\widehat {IDC} = 45^\circ \)
b) Vectơ có điểm đầu là D và điểm cuối là I là \(\overrightarrow {DI} \)
Vectơ có điểm đầu là D và điểm cuối là C là \(\overrightarrow {DC} \)
c) Vectơ có điểm đầu là D và bằng vectơ \(\overrightarrow {IB} \) là \(\overrightarrow {DI} \)
Vectơ có điểm đầu là D và bằng vectơ \(\overrightarrow {AB} \) là \(\overrightarrow {DC} \)

\(\widehat{ABC}=120^0\Rightarrow\widehat{DAB}=180^0-120^0=60^0\)
\(\Rightarrow\Delta ABD\) đều
Gọi E là trung điểm AD \(\Rightarrow\overrightarrow{BE}=\dfrac{1}{2}\overrightarrow{BD}+\dfrac{1}{2}\overrightarrow{BA}\)
\(\Rightarrow\overrightarrow{BG}=\dfrac{2}{3}\overrightarrow{BE}=\dfrac{1}{3}\overrightarrow{BD}+\dfrac{1}{3}\overrightarrow{BA}\)
\(\Rightarrow\overrightarrow{BG}+\overrightarrow{AD}=\dfrac{1}{3}\overrightarrow{BD}+\dfrac{1}{3}\overrightarrow{BA}+\overrightarrow{AD}=\dfrac{1}{3}\left(\overrightarrow{BA}+\overrightarrow{AD}\right)+\dfrac{1}{3}\overrightarrow{BA}+\overrightarrow{AD}\)
\(=\dfrac{2}{3}\overrightarrow{BA}+\dfrac{4}{3}\overrightarrow{AD}=-\dfrac{2}{3}\overrightarrow{AB}+\dfrac{4}{3}\overrightarrow{AD}\)
Đặt \(\overrightarrow{u}=\overrightarrow{BG}+\overrightarrow{AD}\Rightarrow\left|\overrightarrow{u}\right|^2=\left(-\dfrac{2}{3}\overrightarrow{AB}+\dfrac{4}{3}\overrightarrow{AD}\right)=\dfrac{4}{9}AB^2+\dfrac{16}{9}AD^2-\dfrac{16}{9}\overrightarrow{AB}.\overrightarrow{AD}\)
\(=\dfrac{4}{9}.4a^2+\dfrac{16}{9}4a^2-\dfrac{16}{9}.2a.2a.cos60^0=\dfrac{16}{3}a^2\)
\(\Rightarrow\left|\overrightarrow{u}\right|=\dfrac{4a\sqrt{3}}{3}\)

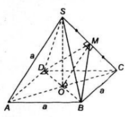
a) Theo giả thiết, S.ABCD là hình chóp đều và đáy ABCD là hình vuông nên SO ⊥ (ABCD) ( tính chất hình chóp đều)
Đáy ABCD là hình vuông cạnh a nên
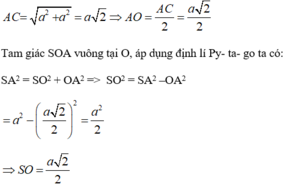

=> Góc giữa hai mặt phẳng (MBD) và (ABCD) là 45 o

Ta có: \(AB = BC = CD = DA = 1;\)
\(AC = BD = \sqrt {A{B^2} + B{C^2}} = \sqrt {{1^2} + {1^2}} = \sqrt 2 \)
a) \(\overrightarrow a = \overrightarrow {OB} - \overrightarrow {OD} = \overrightarrow {OB} + \overrightarrow {DO} = \left( {\overrightarrow {DO} + \overrightarrow {OB} } \right) = \overrightarrow {DB} \)
\( \Rightarrow \left| {\overrightarrow a } \right| = \left| {\overrightarrow {DB} } \right| = DB = \sqrt 2 \)
b) \(\overrightarrow b = \left( {\overrightarrow {OC} - \overrightarrow {OA} } \right) + \left( {\overrightarrow {DB} - \overrightarrow {DC} } \right)\)
\( = \left( {\overrightarrow {OC} + \overrightarrow {AO} } \right) + \left( {\overrightarrow {DB} + \overrightarrow {CD} } \right) = \left( {\overrightarrow {AO} + \overrightarrow {OC} } \right) + \left( {\overrightarrow {CD} + \overrightarrow {DB} } \right)\)
\( = \overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {AB} \)
\( \Rightarrow \left| {\overrightarrow b } \right| = \left| {\overrightarrow {AB} } \right| = AB = 1\)
Chú ý khi giải:
Khi có dấu trừ phía trước ta thường thay bằng vectơ đối của nó và ngược lại
a) \(AC = BD = \sqrt {A{D^2} + D{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
\( \Rightarrow AO = OC = BO = OD = \frac{{a\sqrt 2 }}{2}\)
Suy ra các cặp vectơ bằng nhau và có độ dài bằng \(\frac{{a\sqrt 2 }}{2}\) là:
\(\overrightarrow {AO} \)và \(\overrightarrow {OC} \); \(\overrightarrow {CO} \) và \(\overrightarrow {OA} \); \(\overrightarrow {DO} \) và \(\overrightarrow {OB} \); \(\overrightarrow {OD} \) và \(\overrightarrow {BO} \)
b) Trong hình chỉ có 2 đoạn thẳng AC và BD có độ dài là \(a\sqrt 2\).
Do đó hai vectơ đối nhau và có độ dài bằng \(a\sqrt 2\) là:
\(\overrightarrow {AC} \)và \(\overrightarrow {CA} \); \(\overrightarrow {BD} \) và \(\overrightarrow {DB} \).