Trong y học, một người cân nặng 60 kg chạy với tốc độ 6,5 km/h thì lượng ca-lo tiêu thụ được tính theo công thức: c=4,7t (Nguồn: https://irace.vn).
Trong đó thời gian t được tính theo phút. Hỏi c có phải là hàm số của t không? Vì sao?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
\(t = \dfrac{s}{v}\)
Trong đó: s: quãng đường đi được
v: vận tốc di chuyển
t: thời gian di chuyển

a) Cân nặng chuẩn, chiều cao chuẩn của một bé gái 3 tuổi lần lượt là:
\(C = 9 + 2(3 - 1) = 9 + 2.2 = 13\)(kg);
\(H = 75 + 5(3 - 1) = 75 + 5.2 = 75 + 10 = 85\)(cm).
b) Ta thấy: 13,5 > 13 và 86 > 85. Vậy nên bé gái không đạt tiêu chuẩn (thừa tiêu chuẩn) về cân nặng và chiều cao của Tổ chức Y tế Thế giới.

Ta có:
S = v .t
Trong đó: s: quãng đường đi được
v: vận tốc di chuyển
t: thời gian di chuyển

bài 1: đổi 1h=60 phút
Mỗi km người đó chạy hết :
60:10=6 (phút)
Trên quãng đường dài 7.5 km ,người đó chạy hết:
6\(\times\)7,5 =45(phút)
Bài 2: đổi 1 giờ = 60 phút
Mỗi km , ca nô đi hết số thời gian là :
60:24=2,5(phút)
9km ,ca nô đi hết số thời gian là:
\(2,5\times9=22,5\left(phút\right)\)
Các bài còn lại lm tương tự, tìm 1km đi được bao nhiêu rồi nhân lên
Bài tập 1 :
Thời gian người đó chạy là :
7,5 : 10 = 0,75 ( giờ )
Đổi : 0,75 giờ = 45 phút
Đáp số : 45 phút .
Bài tập 2 :
Thời gian ca nô đi hết quãng đường dài 9km là :
9 : 24 = 0,375 ( giờ )
Đổi : 0,375 giờ = 22,5 phút
Đáp số : 22,5 phút .
Bài tập 3 :
Vận tốc của người đó đi là :
18,3 : 1,5 = 12,2 ( km/h )
Thời gian người đó đi hết quãng đường dài 30,5 km là :
30,5 : 12,2 = 2,5 ( giờ )
Đổi : 2,5 giờ = 2 giờ 30 phút
Đáp số : 2 giờ 30 phút .
Bài tập 4 :
Đổi : 1 giờ 15 phút = 75 phút
1 phút vận động viên đi xe đạp đi được là :
20 : 30 = 2/3 ( km )
75 phút người đó đi được là :
75 \(\times\frac{2}{3}\) = 50 ( km )
Đáp số : 50km .
Học tốt

\(726kJ=726000J\)
\(A=P.t\Rightarrow P=\dfrac{A}{t}=\dfrac{726000}{10.60}=1210\left(W\right)\)
\(P=U.I\Rightarrow I=\dfrac{P}{U}=\dfrac{1210}{220}=5,5\left(A\right)\)
\(R=\dfrac{U}{I}=\dfrac{220}{5,5}=40\left(\Omega\right)\)

Hàm số \(T\left( t \right)\) có tập xác định là \(\left[ {0;100} \right]\).
Ta có: \(T\left( {60} \right) = 10 + 2.60 = 130\)
\(\begin{array}{l}\mathop {\lim }\limits_{t \to {{60}^ + }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{60}^ + }} \left( {k - 3t} \right) = k - 3.60 = k - 180\\\mathop {\lim }\limits_{t \to {{60}^ - }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{60}^ - }} \left( {10 + 2t} \right) = 10 + 2.60 = 130\end{array}\)
Để hàm số liên tục trên tập xác định thì hàm số phải liên tục tại điểm \({t_0} = 60\)
Khi đó: \(\mathop {\lim }\limits_{t \to {{60}^ + }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{60}^ - }} T\left( t \right) = T\left( {60} \right) \Leftrightarrow k - 180 = 130 \Leftrightarrow k = 310\)
Vậy với \(k = 310\) thì hàm số \(T\left( t \right)\) liên tục trên tập xác định.

Đáp án C
Giả sử phương trình parabol có dạng:
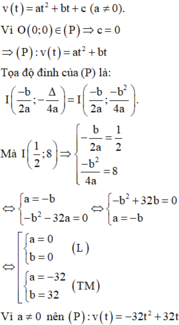
Vậy quãng đường người này chạy được trong 45 phút=0,75h là:
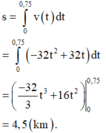

Ta có các biểu thức:
\(s=vt;v=\dfrac{s}{t};t=\dfrac{s}{v}\)
Tất cả đều là đơn thức không phải đa thức
`S = v.t; v = S/t; t = S/v`.
Không phải là đa thức.
c là hàm số của t vì với mỗi giá trị của t thì có 1 và chỉ 1 giá trị của c.