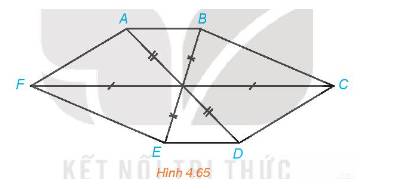
Hình 4.65 có thể là hình biểu diễn của một hình lục giác đều hay không? Vì sao?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
21 tháng 3 2017
Hình 2.67 không thể là hình chiếu song song của hình lục giác đều vì
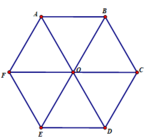
Lục giác đều ABCDEF có O là giao điểm các đường chéo
Ta có: AO // BC
Trên hình 2.67 không biểu diễn được điều đó
(Phép chiếu song song biến hai đường thằng song song thành hai đường thẳng song song hoặc trùng nhau)
CM
31 tháng 12 2019
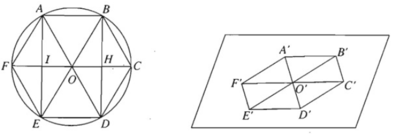
Với hình lục giác đều ABCDEF ta nhận thấy:
- Tứ giác OABC là hình bình hành ( vừa là hình thoi);
- Các điểm D, E, F lần lượt là các điểm đối xứng của các điểm A, B, C qua tâm O
Từ đó suy ra cách vẽ hình biểu diễn của lục giác đều ABCDEF như sau: (h.2.54)
- Vẽ hình bình hành O'A'B'C' biểu diễn cho hình bình hành OABC..
- Lấy các điểm D', E', F' lần lượt đối xứng của A', B', C' qua tâm O', ta được hình biểu diễn A'B'C'D'E'F' của hình lục giác đều ABCDEF.
Chú ý. Ta có thể vẽ hình biểu diễn hình lục giác đều dựa trên sự phân tích sau đây ở hình thực ABCDEF (h.2.53) :
- Tứ giác ABDE là hình chữ nhật;
- Gọi I là trung điểm của cạnh AE và H là trung điểm của cạnh BD;
- Các điểm F và C đối xứng của O lần lượt qua I và H.
Từ đó ta có cách vẽ sau đây:
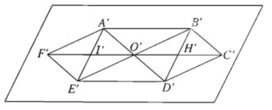
- Vẽ hình bình hành A'B'D'E' biểu diễn cho hình chữ nhật ABDE
- Gọi I' và H' lần lượt là trung điểm của A'E'và B'D'.
- Gọi F' đối xứng với O' qua I' và C' đối xứng với O' qua H', ta được hình biểu diễn A'B'C'D'E'F' của hình lục giác đều.
QT
1
HQ
Hà Quang Minh
Giáo viên
5 tháng 10 2023
Khi sử dụng GeoGebra để vẽ theo hoạt động 5, ta được 6 đoạn thẳng bằng nhau (i = h = m = l = k = j)
Vậy hình lục giác ở hình T.5 là hình lục giác đều.
Hình 4.65 có thể là hình biểu diễn của một hình lục giác đều. Vì nó có 6 cạnh và các đường chéo cắt nhau tại trung điểm của mỗi đường.