Một cấp số cộng cố số hạng đầu bằng 5 và công sai bằng 2. Hỏi phải lấy tổng của bao nhiêu số hạng đầu của cấp số cộng này để có tổng bằng 2700?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
Ta có: \({S_n} = \frac{{5\left( {1 - {2^n}} \right)}}{{1 - 2}} = - 5 + 5 \times {2^n}\;\)
\(\begin{array}{l}5115 = - 5 + {5.2^n}\\ \Leftrightarrow {2^n} = 1024 = 2.\\ \Rightarrow n = 10.\end{array}\)
Vậy phải lấy tổng 10 số hạng đầu.
BT
25 tháng 5 2017
Gọi ba số đó là \(x,y,z\). Do ba số là các số hạng thứ hai, thứ 9 và thứ 44 của một cấp số cộng nên:
\(x;y=x+7d;z=x+42d\). (Với d là công sai của cấp số cộng).
Ta có: \(x+y+z=x+x+7d+x+42d=3x+49d=217\).
Mặt khác x, y, z là các số hạng liên tiếp của một cấp số nhân nên:
\(y^2=xz\)\(\Leftrightarrow\left(x+7d\right)^2=x\left(x+42d\right)\)\(\Leftrightarrow-28xd+49d^2=0\)\(\Leftrightarrow7d\left(-4x+7d\right)=0\)\(\Leftrightarrow\left[{}\begin{matrix}d=0\\-4x+7d=0\end{matrix}\right.\).
Với \(d=0\) suy ra \(x=y=z=\dfrac{217}{3}\).
Suy ra: \(n=820:\dfrac{217}{3}=\dfrac{2460}{217}\notin N\).
Với \(4+7d=0\). Ta có hệ:
\(\left\{{}\begin{matrix}4x+7d=0\\3x+49d=217\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=7\\d=4\end{matrix}\right.\).
Vậy \(u_1=7-4=3\).
Có \(S_n=\dfrac{\left[2u_1+\left(n-1\right)d\right]n}{2}=\dfrac{\left[2.3+\left(n-1\right)4\right]n}{2}=820\)
\(\Rightarrow n=20\left(tm\right)\).
CM
7 tháng 4 2018
u 12 = 23 S 12 = 144 ⇒ u 1 + 11 d = 23 12 2 u 1 + u 12 = 144 ⇔ u 1 + 11 d = 23 u 1 + 23 = 24 ⇔ u 1 = 1 d = 23 − u 1 11 = 2
Chọn đáp án A
CM
23 tháng 12 2019
Chọn C
- Do công sai và số hạng đầu là d = 1, u 1 = 1 nên đây là tổng của n số tự nhiên đầu tiên là:
27 tháng 10 2023
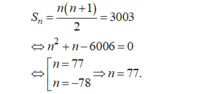
Theo đề, ta có: \(S_n=3003\)
=>\(n\cdot\dfrac{\left[2u1+\left(n-1\right)\cdot d\right]}{2}=3003\)
=>\(\dfrac{n\left[2+\left(n-1\right)\right]}{2}=3003\)
=>n(n+1)=6006
=>n^2+n-6006=0
=>(n-77)(n+78)=0
=>n=77(nhận) hoặc n=-78(loại)
Vậy: n=77
Ta có: \({S_n} = \frac{n}{2}\left[ {2 \times 5 + \left( {n - 1} \right) \times 2} \right] = 2700\;\)
\( \Leftrightarrow \frac{n}{2}\left( {8 + 2n} \right) = 2700\;\)
\( \Leftrightarrow {n^2} + 4n - 2700 = 0\;\)
\( \Leftrightarrow \left[ \begin{array}{l}n = - 54(L)\\n = 50(TM)\end{array} \right.\)
Vậy phải lấy tổng 50 số hạng đầu