Hai con lắc đơn có chiều dài lần lượt là l1 và l2 thì chu kì dđ tương ứng là T1 và T2. Nếu con lắc có chiều dài bằng l1 + l2 thì chu kì dđ của con lắc là 2,7s. Nếu con lắc có chiều dài bằng l1 - l2 thì chu kì dd0 của con lắc là 0,9s. Chu kì T1 và T2 là?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

7 tháng 7 2019
[Vật lí 12] con lắc đơn | Cộng đồng học sinh Việt Nam
A
7 tháng 7 2019
Ta có biểu thức của các chu kì :
\(T_1=2\pi\sqrt{\frac{l_1}{g}};T_2=2\pi\sqrt{\frac{l_2}{g}};T=2\pi\sqrt{\frac{l_1+l_2}{g}};T'=\sqrt{\frac{l_1-l_2}{g}}\)
\(\Rightarrow\frac{l_1}{T_1^2}=\frac{l_2}{T_2^2}=\frac{l_1+l_2}{T^2}=\frac{l_1-l_2}{T'^2}\)
Vậy \(T_1^2+T_2^2=T^2\) và \(T_1^2-T_2^2=T'^2\)
Do đó : \(T_1=\sqrt{\frac{T^2+T'^2}{2}}=\sqrt{\frac{2,7^2+0,9^2}{2}}\approx2,0\left(s\right)\)
\(T_2=\sqrt{\frac{T^2-T'^2}{2}}=\sqrt{\frac{2,7^2-0,9^2}{2}}\approx1,8\left(s\right)\)
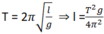
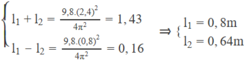
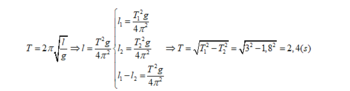
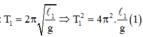
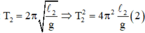
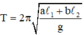
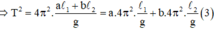
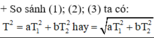
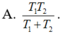
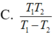
\(T=2\pi\sqrt{\dfrac{l}{g}}\Rightarrow T^2\) tỉ lệ thuận với l
Theo bài ra
\(\left\{{}\begin{matrix}T_1^2+T_2^2=\left(2,7\right)^2=7,29\\T_1^2-T_2^2=\left(0,9\right)^2=0,81\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}T_1^2=4,05\\T_2^2=3,24\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}T_1=2,01s\\T_2=1,8s\end{matrix}\right.\)