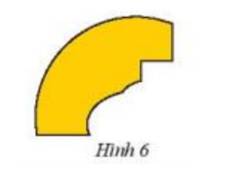
Người ta muốn phục chế lại một đĩa cổ hình tròn bị vỡ chỉ còn lại một mảnh (Hình 6). Làm thế nào để các định được bán kính của đĩa cổ này?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi phần cung tròn bị cắt có góc ở tâm bằng x độ \(\left(0< x< 360\right)\)
Chu vi đường tròn ban đầu: \(2\pi R\)
Chu vi sau khi bị cắt: \(2\pi R\left(1-\dfrac{x}{360}\right)\)
(Và lưu ý chu vi này đúng bằng chu vi đường tròn đáy hình nón được tạo ra, đường sinh nón bằng R)
Gọi đáy nón có bán kính \(r\)
\(\Rightarrow2\pi r=2\pi R\left(1-\dfrac{x}{360}\right)\Rightarrow r=R\left(1-\dfrac{x}{360}\right)\)
\(\Rightarrow V_{nón}=\dfrac{1}{3}\pi r^2.\sqrt{R^2-r^2}=f\left(x\right)\)
Giờ chắc khảo sát hàm \(f\left(x\right)\) tìm x là được

Đáp án A
Ta có thể nhận thấy đường sinh của hình nón là bán kính của đĩa tròn. Còn chu vi đáy của hình nón chính là chu vi của đĩa trừ đi độ dài cung tròn đã cắt. Như vậy ta tiến hành giải chi tiết như sau:


![]()
Gọi x là khoảng cách từ tâm hình tròn lớn O đến trọng tâm phần còn lại O1.
Theo quy tắc hợp lực song song:
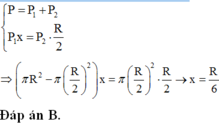

Giả sử ta khoét thêm một lỗ tròn bán kính R/2 nữa đối xứng với lỗ tròn đã khoét lúc đầu (H.III.6G)
Gọi P → là trọng lượng của đĩa bán kính R khi chưa bị khoét, P 1 → là trọng lượng của đĩa nhỏ có bán kính R/2 và P 2 → là trọng lượng của phần đĩa còn lại sau hai lần khoét, ta có:
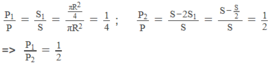
Do tính chất đối xứng, trọng tâm phần đĩa còn lại sau hai lần khoét thì trùng với tâm O của đĩa khi chưa khoét, còn trọng tâm của đĩa nhỏ mà ta giả sử khoét thêm thì ở tâm O 1 của nó. Gọi G là trọng tâm của đĩa sau khi bị khoét một lỗ tròn. Ta có hệ phương trình
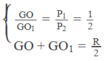
Giải ra ta được: G O 1 = R/3 và GO = R/6

sau khi vo con lai so cai dia la : 600 - 69 = 551( cai )
moi cai dia con lai ban voi gia 6000 dong thi ban duoc so tien la : 6000 x 551 = 30 306 000 ( dong )
nguoi do lai duoc la : 30 306 000 : 100 x 18 = 5455080 ( dong )
tien von mua 600 cai dia la : 30 306 000 + 5 455 080 = ______
Gọi O là tâm của chiếc đĩa
\( \Rightarrow \) OA = OB = OC = r ( do cùng có độ dài = bán kính )
Xét tam giác ABC có O là điểm cách đều A, B, C
\( \Rightarrow \) O là giao của 3 đường trung trực tam giác ABC
Để xác định O ta vẽ 2 đường trung trực của AB, BC chúng cắt nhau tại O .