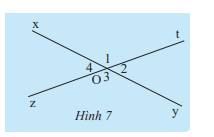
Cho hai đường thẳng xy và zt cắt nhau tại O (Hình 7). Ta gọi tia Oy là tia đối của tia Ox và gọi tia Ot là tia đối của tia Oz. Hãy cho biết quan hệ về cạnh, quan hệ về đỉnh của \(\widehat {{O_1}}\) và \(\widehat {{O_3}}\).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Đỉnh của góc xOz và zOy cùng là đỉnh O
2 góc xOz và zOy có chung cạnh Oz, cạnh còn lại (Ox và Oy) là 2 tia đối nhau.
b) \(\widehat{xOz}=40^0, \widehat{zOy}=140^0\)
Ta được: \(\widehat{xOz}+\widehat{zOy}=40^0+140^0=180^0\)

a) Cạnh Ox của góc xOz là tia đối của cạnh Oy của góc yOt.
b) Cạnh Oz của góc xOz là tia đối của cạnh Ot của góc yOt.

a) Đỉnh của góc xOy và zOy cùng là đỉnh O; cạnh chung là cạnh Oy.
b)
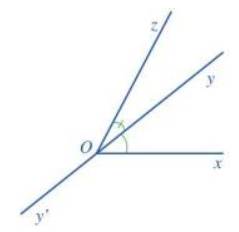
c) Hai tia Ox và Oz nằm về hai phía của đường thẳng yy’

1. Cho xOy = 135. Trên nửa mặt phẳng bờ Oy chứa Ox, vẽ tia Oz sao cho góc yOz vuông. Gọi Ot là tia đối của tia Oz. Khi đó xOt = 135
2. Cho đường thẳng xy. Trên đường thẳng xy lấy O. Trên cùng một nửa mặt phẳng bờ xy vẽ các tia Om và On sao cho xOm và mOn là hai góc kề nhau. Biết xOm = 2mOn = 6nOy. Vậy mOn = 54
100 % chính xác!

nếu giỏi thì làm cả lời giải hắn hỏi khi đó mới tích chứ không tích bừa
\(\widehat {{O_1}}\) có cạnh Ox và Ot, đỉnh O
\(\widehat {{O_3}}\) có cạnh Oy và Oz, đỉnh O
Ta có: \(\widehat {{O_1}}\) và \(\widehat {{O_3}}\) có mỗi cạnh của góc này là cạnh đối của một cạnh của góc kia.
\(\widehat {{O_1}}\) và \(\widehat {{O_3}}\) có chung đỉnh