Gọi A và A' lần lượt là hai điểm biểu diễn hai số 4,5 và -4,5 trên trục số. So sánh OA và OA'.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 10 2021
a: Xét tứ giác ABCD có
M là trung điểm của BD
M là trung điểm của AC
Do đó: ABCD là hình bình hành
mà \(\widehat{BAD}=90^0\)
nên ABCD là hình chữ nhật
22 tháng 10 2023
a: ABCD là hình bình hành
=>\(\widehat{BAD}+\widehat{ABC}=180^0;\widehat{ABC}+\widehat{BCD}=180^0;\widehat{ADC}+\widehat{BCD}=180^0;\widehat{BAD}+\widehat{ADC}=180^0\)
\(\widehat{BAD}+\widehat{ABC}=180^0\)
=>\(2\cdot\left(\widehat{MAB}+\widehat{MBA}\right)=180^0\)
=>\(\widehat{MAB}+\widehat{MBA}=90^0\)
=>\(\widehat{AMB}=90^0\)
=>AM vuông góc MB
=>AN vuông góc BQ
b: \(\widehat{ADC}+\widehat{BCD}=180^0\)
=>\(2\cdot\left(\widehat{PDC}+\widehat{PCD}\right)=180^0\)
=>\(\widehat{PDC}+\widehat{PCD}=90^0\)
=>ΔPCD vuông tại P
=>\(\widehat{CPD}=90^0\)
=>\(\widehat{NPQ}=90^0\)
\(\widehat{BAD}+\widehat{ADC}=180^0\)
=>\(2\cdot\left(\widehat{NAD}+\widehat{NDA}\right)=180^0\)
=>\(\widehat{NAD}+\widehat{NDA}=90^0\)
=>ΔNAD vuông tại N
=>\(\widehat{AND}=90^0\)
=>\(\widehat{MNP}=90^0\)
Xét tứ giác MNPQ có
\(\widehat{MNP}=\widehat{NMQ}=\widehat{NPQ}=90^0\)
=>MNPQ là hình chữ nhật
6 tháng 4 2021
a) Áp dụng định lí Pytago vào ΔAHB vuông tại H, ta được:
\(AB^2=AH^2+HB^2\)
\(\Leftrightarrow AB^2=6^2+8^2=100\)
hay AB=10(cm)
Áp dụng định lí Pytago vào ΔAHC vuông tại H, ta được:
\(AC^2=AH^2+HC^2\)
\(\Leftrightarrow AC^2=6^2+10^2=136\)
hay \(AC=2\sqrt{34}cm\)
Ta có: AB=10cm
\(AC=2\sqrt{34}cm\)
mà \(10cm< 2\sqrt{34}cm\)
nên AB<AC
15 tháng 5 2021
a) Xét (O) có
\(\widehat{EFC}\) là góc nội tiếp chắn cung EC
\(\widehat{ACE}\) là góc tạo bởi tiếp tuyến CA và dây cung CE
Do đó: \(\widehat{EFC}=\widehat{ACE}\)(Hệ quả góc tạo bởi tiếp tuyến và dây cung)
hay \(\widehat{ACE}=\widehat{AFC}\)
Xét ΔACE và ΔAFC có
\(\widehat{ACE}=\widehat{AFC}\)(cmt)
\(\widehat{EAC}\) chung
Do đó: ΔACE\(\sim\)ΔAFC(g-g)
Suy ra: \(\dfrac{AC}{AF}=\dfrac{AE}{AC}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AC^2=AE\cdot AF\)(Đpcm)
15 tháng 5 2021
b) Xét ΔOEF có OE=OF(=R)
nên ΔOEF cân tại O(Định nghĩa tam giác cân)
Ta có: ΔOEF cân tại O(Cmt)
mà OI là đường trung tuyến ứng với cạnh đáy EF(I là trung điểm của EF)
nên OI là đường cao ứng với cạnh EF(Định lí tam giác cân)
\(\Leftrightarrow OI\perp EF\)
Ta có: \(\widehat{OIA}=90^0\left(OI\perp EF\right)\)
nên I nằm trên đường tròn đường kính OA(1)
Ta có: \(\widehat{OBA}=90^0\left(gt\right)\)
nên B nằm trên đường tròn đường kính OA(2)
Ta có: \(\widehat{OCA}=90^0\left(gt\right)\)
nên C nằm trên đường tròn đường kính OA(3)
Từ (1), (2) và (3) suy ra A,B,O,I,C cùng nằm trên một đường tròn(đpcm)
CM
4 tháng 12 2019
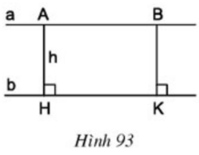
AH // BK (cùng ⊥ b) và AB // HK ⇒ tứ giác ABKH là hình bình hành
⇒ AH = BK = h
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
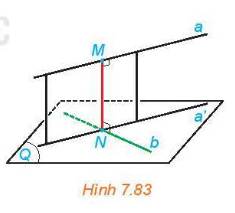
a) Mặt phẳng chứa a và a' có vuông góc với (Q)
b) Ta có \(MN \bot \left( Q \right),b \subset \left( Q \right) \Rightarrow MN \bot b\)
\(MN \bot a\) (M là hình chiếu của N trên a)
Vậy MN có vuông góc với cả hai đường thẳng a và b.
c) Vì a // (Q) nên d(a, (Q)) = d(M, (Q)) = MN
24 tháng 1 2021
a) Ta có: \(\widehat{ABH}=\widehat{HBC}=\dfrac{\widehat{ABC}}{2}\)(BH là tia phân giác của \(\widehat{ABC}\))
\(\widehat{ACK}=\widehat{BCK}=\dfrac{\widehat{ACB}}{2}\)(CK là tia phân giác của \(\widehat{ACB}\))
mà \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy của ΔABC cân tại A)
nên \(\widehat{ABH}=\widehat{HBC}=\widehat{ACK}=\widehat{BCK}\)
Xét ΔABH và ΔACK có
\(\widehat{BAH}\) chung
AB=AC(ΔABC cân tại A)
\(\widehat{ABH}=\widehat{ACK}\)(cmt)
Do đó: ΔABH=ΔACK(g-c-g)
Ta có: OA = 4,5 và OA’=4,5 nên OA=OA’.