Hãy mô tả lại các bước đã thực hiện trong phép chia đa thức D cho đa thức E.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
24 tháng 11 2019
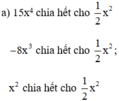
Do đó A = 15x4 - 8x3 + x2 chia hết cho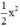 
hay A chia hết cho B.
b) A = x2 - 2x + 1 = (x – 1)2
Vậy A chia hết cho x – 1 hay A chia hết cho B.
11 tháng 3 2023
a: \(\dfrac{A}{B}=\dfrac{x^3+4x^2+3x+12-19}{x+4}=x^2+3+\dfrac{-19}{x+4}\)
b: Để A chia hết cho B thì \(x+4\in\left\{1;-1;19;-19\right\}\)
=>\(x\in\left\{-3;-5;15;-23\right\}\)
19 tháng 12 2021
Bài 1:
a: \(=\dfrac{2x^4-8x^3+2x^2+2x^3-8x^2+2x+18x^2-72x+18+56x-15}{x^2-4x+1}\)
\(=2x^2+2x+18+\dfrac{56x-15}{x^2-4x+1}\)
14 tháng 12 2022
a: \(\dfrac{A}{B}=\dfrac{x^3+x^2+2x^2+2x+x+1-3}{x+1}=x^2+2x+1-\dfrac{3}{x+1}\)
b: Để A chia hết cho B thì \(x+1\in\left\{1;-1;3;-3\right\}\)
=>\(x\in\left\{0;-2;2;-4\right\}\)
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
Để thực hiện phép chia một đa thức cho một đa thức khác, ta làm như sau:
Bước 1:
- Chia đơn thức bậc cao nhất của đa thức bị chia cho đơn thức bậc cao nhất của đa thức chia.
- Nhân kết quả trên với đa thức chia và đặt tích dưới đa thức bị chia sao cho hai đơn thức có cùng số mũ của biến ở cùng cột.
- Lấy đa thức bị chia trừ đi tích đặt dưới để được đa thức mới.
Bước 2: Tiếp tục quá trình trên cho đến khi nhận được đa thức không hoặc đa thức có bậc nhỏ hơn bậc của đa thức chia.
N
1
2 tháng 12 2021
\(=\left(x^4-x^3+x^2+x^3-x^2+x+3x^2-3x+3+2018\right):\left(x^2-x+1\right)\\ =\left[\left(x^2-x+1\right)\left(x^2+x+3\right)+2018\right]:\left(x^2-x+1\right)\\ =x^2+x+3\left(\text{dư 2018}\right)\)
7 tháng 11 2021
\(\dfrac{A}{B}=\dfrac{8x^3+2x^2-8x-2-3}{4x+1}\)
\(=2x^2-2-\dfrac{3}{4x+1}\)
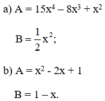
Bước 1: Đặt tính chia tương tự như chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của D chia cho hạng tử bậc cao nhất của E.
Bước 2: Lấy D trừ đi tích của E với thương mới thu được ở bước 1
Bước 3: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của E
Bước 4: Lấy dư thứ nhất trừ đi tích E với thương vừa thu được ở bước 3. Ta được dư thứ hai có bậc nhỏ hơn bậc của E thì quá trình chia kết thúc.