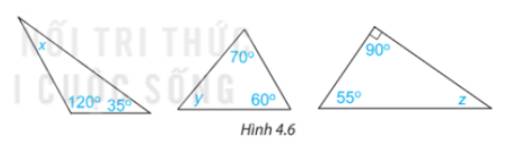
Tính các số đo x, y ,z trong Hình 4.6
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 9 2023
x=180-120-35=180-155=25 độ
y=180-70-60=50 độ
z=180-90-55=35 độ
18 tháng 9 2023
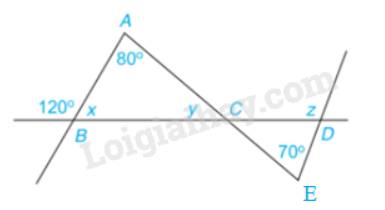
Ta có:
\(x + {120^o} = {180^o}\)( 2 góc kề bù)
\(\begin{array}{l} \Rightarrow x = {180^o} - {120^o}\\ \Rightarrow x = {60^o}\end{array}\)
Áp dụng định lí tổng các góc trong tam giác ABC, có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\\ \Rightarrow {80^o} + {60^o} + y = {180^o}\\ \Rightarrow y = {40^o}\end{array}\)
Ta có: \(\widehat {DCE} = y = {40^o}\)(đối đỉnh)
Áp dụng định lí tổng các góc trong tam giác CDE, có:
\(\begin{array}{l}\widehat C + \widehat D + \widehat E = {180^o}\\ \Rightarrow {40^o} + \widehat D + {70^o} = {180^o}\\ \Rightarrow \widehat D = {70^o}\end{array}\)
Mà \(\widehat D + z = {180^o}\)( 2 góc kề bù)
\( \Rightarrow z = {180^o} - {70^o} = {110^o}\)
15 tháng 10 2023
ta có x + 120* =180*(2 góc kề bù)
=> x= 180*-120*
= 60*
Ta có A+X+Y =180*
=> Y = 180*- A - X
= 180* - 80* - 60*
= 40*
ta có Y = ZCE = 40* (2 góc đối đỉnh)
Ta có Z = E + ZCE(định lý tổng 3 góc của TG )
=>Z = 70*+40*
=110*
QT
1
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
a) Vì m // n nên x = 135\(^\circ \)( 2 góc đồng vị) ; y = 80\(^\circ \) ( 2 góc so le trong)
b)
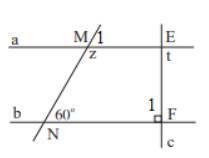
Vì a // b nên \(\widehat {{M_1}} = 60^\circ \) ( 2 góc đồng vị)
Mà \(\widehat {{M_1}} + z = 180^\circ \) ( 2 góc kề bù) nên z = 180\(^\circ \)- 60\(^\circ \)=120\(^\circ \)
Vì a // b nên \(\widehat {{F_1}} = t\) ( 2 góc so le trong), mà \(\widehat {{F_1}} = 90^\circ \) nên t = 90\(^\circ \)
Áp dụng định lí tổng ba góc trong tam giác, ta có:
+)
\(\begin{array}{l}x + {120^o} + {35^o} = {180^o}\\ \Rightarrow x + {155^o} = {180^o}\\ \Rightarrow x = {180^o} - {155^o}\\ \Rightarrow x = {25^o}\end{array}\)
+)
\(\begin{array}{l}y + {70^o} + {60^o} = {180^o}\\ \Rightarrow y = {180^o} - {70^o} - {60^o}\\ \Rightarrow y = {50^o}\end{array}\)
+)
\(\begin{array}{l}z+ {90^o} + {55^o} = {180^o}\\ \Rightarrow z = {180^o} - {90^o} - {55^o}\\ \Rightarrow z = {35^o}\end{array}\)